Расчетная модель упорного подшипника скольжения с повышенной несущей способностью, работающего на неньютоновских смазочных материалах с адаптированной опорной поверхностью
Аннотация
Дата поступления статьи: 21.10.2013Умение правильно выбирать противоизносные присадки [1–6] позволяет создать смазочные материалы, которые в тонких слоях обладают иными свойствами, чем в больших объемах. Обычно принято считать, что присадки функционируют лишь в зоне граничной смазки и не входят в область гидродинамической теории смазки. Однако, благоприятное влияние присадок как указывается во многих работах [1-5] имеет место в режиме «тонкого слоя» гидродинамической смазки.
Как известно, подшипники жидкостного трения работают на разных видах смазочных материалов, которые состоят из масляной основы и композиции присадок, обеспечивающих маслу необходимые функциональные свойства. Добавки полимеров с высоким молекулярным весом придают маслам вязкоупругие свойства. Анализ существующих работ [7–9], посвященных расчету подшипников скольжения, работающих на вязкоупругой смазке, показывает, что в них не учитывается зависимость вязкости и модуля сдвига от давления и температуры, а режим трения предполагается ламинарным. Как известно [10], высокоскоростные подшипники работают в турбулентном режиме трения, более высоким повышенным давлением и температуры и поэтому разработка методов расчета подшипников скольжения, работающих на вязкоупругой смазке требует учета выше указанных факторов.
В связи с выше написанным приведем сначала разработку расчетной модели упорных подшипников, работающих на микрополярной смазке с учетом вязкостных характеристик этих смазок от давления в отличие от существующих расчетных моделей, не учитывающих этих зависимостей (задача 1).
А затем рассмотрим расчетную модель упорного подшипника повышенной несущей способности, работающего на вязкоупругой смазке с учетом зависимости ее характеристик от давления (задача 2).Ключевые слова: упорный подшипник с адаптированной упорной поверхностью, неньютоновские смазочные материалы
Умение правильно выбирать противоизносные присадки [1–6] позволяет создать смазочные материалы, которые в тонких слоях обладают иными свойствами, чем в больших объемах. Считается, что присадки функционируют лишь в зоне граничной смазки и, тем самым, не входят в область гидродинамической теории смазки. Однако, благоприятное влияние присадок как указывается во многих работах [1-5] имеет место в режиме «тонкого слоя» гидродинамической смазки.
Как известно, подшипники жидкостного трения работают на разных видах смазочных материалов, которые состоят из масляной основы и композиции присадок, обеспечивающих маслу необходимые функциональные свойства. При добавлении полимеров с высоким молекулярным весом масла приобретают вязкоупругие свойства. Анализ существующих работ [7–9], посвященных расчету подшипников скольжения, работающих на вязкоупругой смазке, показывает, что в них не учитывается зависимость вязкости и модуля сдвига от давления и температуры, а режим трения предполагается ламинарным. Как известно [10], высокоскоростные подшипники работают в турбулентном режиме трения, более высоким повышенным давлением и температуры и поэтому разработка методов расчета подшипников скольжения, работающих на вязкоупругой смазке требует учета выше указанных факторов.
В связи с выше написанным приведем сначала разработку расчетной модели упорных подшипников, работающих на микрополярной смазке с учетом вязкостных характеристик этих смазок от давления в отличие от существующих расчетных моделей, не учитывающих этих зависимостей (задача 1).
А затем рассмотрим расчетную модель упорного подшипника повышенной несущей способности, работающего на вязкоупругой смазке с учетом зависимости ее характеристик от давления (задача 2).
1. Постановка задачи 1. Рассмотрим установившееся движение жидкости, обладающей микрополярными свойствами, в зазоре упорного подшипника (между ползуном и направляющей). Предполагается, что ползун неподвижен, а направляющая движется со скоростью ![]() по направлению оси
по направлению оси ![]() (рис. 1.1). Также предполагается, что вязкостные характеристики микрополярной жидкости зависят от давления
(рис. 1.1). Также предполагается, что вязкостные характеристики микрополярной жидкости зависят от давления
![]() .(1.1)
.(1.1)
Здесь ![]() – характерная вязкость ньютоновской смазки;
– характерная вязкость ньютоновской смазки; ![]() и
и ![]() – характерные вязкости микрополярной смазки;
– характерные вязкости микрополярной смазки; ![]() – гидродинамическое давление;
– гидродинамическое давление; ![]() – экспериментальная постоянная величина.
– экспериментальная постоянная величина.
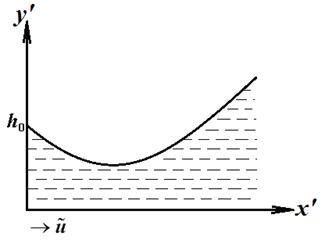
Рис. 1.1 Схематическое изображение пары трения «ползун-направляющая» с адаптированным профилем ползуна
В декартовой системе координат ![]() уравнение контура направляющей и ползуна можно записать в виде:
уравнение контура направляющей и ползуна можно записать в виде:
![]() , (1.2)
, (1.2)
где ![]() – угол наклона ползуна с линейным контуром к оси
– угол наклона ползуна с линейным контуром к оси ![]() ;
; ![]() и
и ![]() будем считать малыми величинами одного порядка;
будем считать малыми величинами одного порядка; ![]() – подлежит определению.
– подлежит определению.
2. Основные уравнения и граничные условия задачи 1.
Учитывая зависимость вязкости от давления в качестве основных уравнений рассмотрим систему безразмерных уравнений движения смазочного материала, обладающего микрополярными свойствами, для «тонкого слоя» с учетом (1.1) и уравнение неразрывности
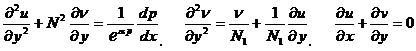 . (1.3)
. (1.3)![]()
Приведем связь размерных величин ![]() с безразмерными величинами
с безразмерными величинами ![]() :
:
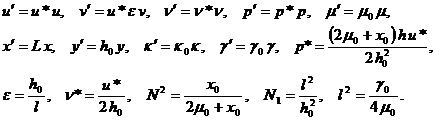
![]()
![]() (1.4)
(1.4)
Здесь ![]() – длина ползуна;
– длина ползуна; ![]() – скорость микровращения;
– скорость микровращения; ![]() – компоненты вектора скорости.
– компоненты вектора скорости.
Обозначим ![]() , тогда
, тогда 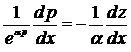 .
.
Учитывая, что параметр ![]() решение задачи (1.3)-(1.5) будем искать в виде рядов по степеням малого параметра
решение задачи (1.3)-(1.5) будем искать в виде рядов по степеням малого параметра ![]()
![]() .(1.6)
.(1.6) ![]()
Подставим (1.6) в (1.3), тогда для нулевого приближения получим систему уравнений и граничных условий к ним 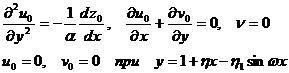 ; (1.7)
; (1.7)
![]() . (1.8)
. (1.8)
Для задач (1.7)-(1.8) автомодельное решение ищем в явном виде
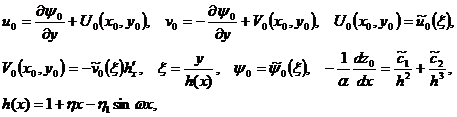 (1.9)
(1.9)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() являются решением следующей задачи
являются решением следующей задачи
![]() (1.10)
(1.10)
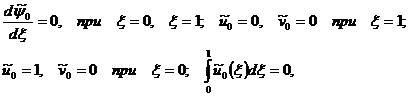 (1.11)
(1.11)
где ![]()
![]() определяется из условия
определяется из условия ![]() .
.
Решение системы уравнений (1.10)-(1.11) найдем непосредственным интегрированием. В результате будем иметь
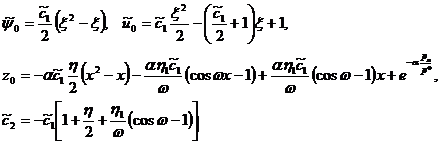 (1.12)
(1.12)
Приведем системе уравнений и граничных условий к ним для первого приближения:
![]() (1.13)
(1.13)
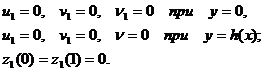 (1.14)
(1.14)
После необходимых вычислений решение задачи запишется в виде
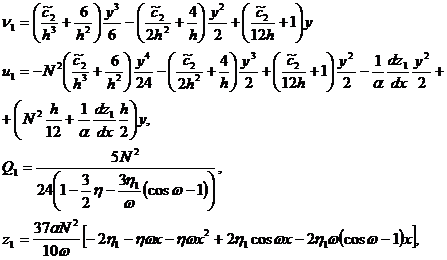 (1.15)
(1.15)
где ![]() - добавочный безразмерный расход, обусловленный микрополярными свойствами смазочной жидкости.
- добавочный безразмерный расход, обусловленный микрополярными свойствами смазочной жидкости.
Для определения гидродинамического давления имеем
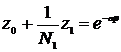 (1.16)
(1.16)
Воспользуемся асимптотическим разложением функции ![]() в принятом нами приближении
в принятом нами приближении ![]() ,
, 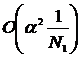 , получим следующее выражение
, получим следующее выражение
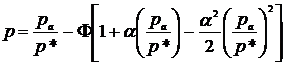 (1.17)
(1.17)
где 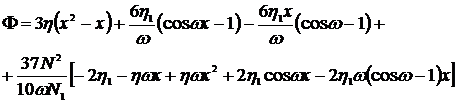 (2.6.18)
(2.6.18)
Используя (1.17) и (1.18), для безразмерной несущей способности будем иметь
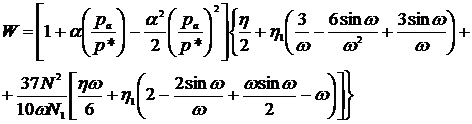 (1.19)
(1.19)
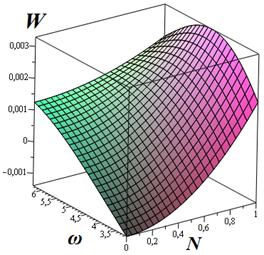
Приведем результаты численного анализа (рис. 1.2-1.3) найденного аналитического выражения для несущей способности подшипника:
1. Несущая способность подшипника существенно зависит от параметров микрополярного смазочного материала ![]() и
и ![]() , а также от параметра
, а также от параметра ![]() , обусловленного зависимостью вязкостных характеристик от давления.
, обусловленного зависимостью вязкостных характеристик от давления.
2. С увеличением значений параметра ![]() несущая способность подшипника возрастает.
несущая способность подшипника возрастает.
3. С увеличением значений параметра ![]() несущая способность подшипника снижается. При
несущая способность подшипника снижается. При ![]() значение несущей способности стремится к соответствующему значению несущей способности для случая ньютоновского смазочного материала.
значение несущей способности стремится к соответствующему значению несущей способности для случая ньютоновского смазочного материала.
4. С увеличением значений параметра ![]() несущая способность подшипника возрастает. При значении
несущая способность подшипника возрастает. При значении ![]() в зависимости несущей способности от
в зависимости несущей способности от ![]() наблюдается ярко выраженный максимум.
наблюдается ярко выраженный максимум.
5. Наиболее рациональными по несущей способности являются значения параметров ![]()
![]() .
.
6. При значении параметра ![]() близком к
близком к ![]() рассматриваемый радиальный подшипник (по сравнению с
рассматриваемый радиальный подшипник (по сравнению с ![]() ) обладает свойством подшипника, так называемого, «двойного действия», по несущей способности.
) обладает свойством подшипника, так называемого, «двойного действия», по несущей способности.
|
|
|
|
Рис. 1.2. Зависимость безразмерной несущей способности упорного подшипника от параметров |
Рис. 1.3. Зависимость безразмерной несущей способности упорного подшипника от параметров |
Рассмотрим теперь расчетную модель упорного подшипника повышенной несущей способности, работающего на вязкоупругой смазке с учетом зависимости ее характеристик от давления (задача 2).
1. Постановка задачи 2. Рассматривается установившееся движение смазки, обладающей вязкоупругими свойствами, между направляющей и ползуном. Предполагается, что ползун неподвижен, а направляющая движется со скоростью ![]() по направлению оси
по направлению оси ![]() . Также предполагается, что зависимость вязкости и модуля сдвига давления выражаются формулами
. Также предполагается, что зависимость вязкости и модуля сдвига давления выражаются формулами
![]() ,(2.1)
,(2.1)
где ![]() – характерная вязкость;
– характерная вязкость; ![]() – характерное значение модуля сдвига;
– характерное значение модуля сдвига; ![]() – динамический коэффициент вязкости;
– динамический коэффициент вязкости; ![]() – гидродинамическое давление;
– гидродинамическое давление; ![]() – экспериментальная постоянная величина.
– экспериментальная постоянная величина.
В декартовой системе координат ![]() уравнение контуров направляющей и ползуна можно записать в виде:
уравнение контуров направляющей и ползуна можно записать в виде:
![]() .(2.2)
.(2.2)
Здесь ![]() – угол наклона ползуна с линейным контуром к оси
– угол наклона ползуна с линейным контуром к оси ![]() ;
; ![]() и
и ![]() – малые безразмерные величины одного порядка;
– малые безразмерные величины одного порядка; ![]() – толщина пленки в начальном сечении;
– толщина пленки в начальном сечении; ![]() – подлежит определению.
– подлежит определению.
В дальнейшем для решения рассматриваемой задачи сделаем следующие общепринятые допущения:
- В качестве смазочного материала рассмотрим неньютоновскую жидкость вместо ньютоновской смазки.
- Давление
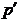 постоянно по толщине пленки, заданной уравнением (2.2).
постоянно по толщине пленки, заданной уравнением (2.2). - Характеристики применяемой максвелловской жидкости выражаются следующим уравнением [7-9]
![]() . (2.3)
. (2.3)
В случае установившихся условий производную ![]() , фигурирующую в уравнении (2.3), можно заменить производной
, фигурирующую в уравнении (2.3), можно заменить производной ![]() . Следовательно, характеристики потока приближенно выражаются уравнением
. Следовательно, характеристики потока приближенно выражаются уравнением
![]() , (2.4)
, (2.4)
в котором ![]() – скорость движения направляющей,
– скорость движения направляющей, ![]() – касательное напряжение.
– касательное напряжение.
2. Основные уравнения и граничные условия задачи 2
В рамках приведенных допущений уравнение равновесия жидкостного элемента, расположенного между поверхностями упорного подшипника, записывается в виде
![]() , (2.5)
, (2.5)
где ![]() – гидродинамическое давление.
– гидродинамическое давление.
После интегрирования вышеуказанного уравнения, получим
![]() .
.
Запишем градиент скорости для максвелловской жидкости с характеристиками потока (2.4)
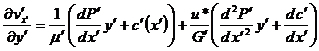 , (2.6)
, (2.6)
Продифференцируем обе части уравнения (2.6) по ![]() , тогда получим
, тогда получим
![]() , (2.7)
, (2.7)
В качестве исходных уравнений рассмотрим уравнение неразрывности и уравнение (2.7)
![]() .(2.8)
.(2.8)
Осуществим переход к безразмерным переменным:
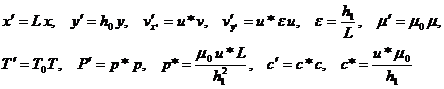 , (2.9)
, (2.9)
где ![]() – длина ползуна;
– длина ползуна; ![]() – толщина пленки в начальном сечении.
– толщина пленки в начальном сечении.
Подставляя (2.9) в (2.7) и (2.8), получим:
![]() , (2.10)
, (2.10)
![]() , (2.11)
, (2.11)
где ![]() – число Дебора.
– число Дебора.
![]() .
.
Выпишем граничные условия для решения системы дифференциальных уравнений (2.10) и (2.11), определяющие прилипание смазочного материала к поверхности ползуна ![]() .
.
прилипание смазочного материала к направляющей поверхности
![]() .
.
условия, накладываемые на давление на торцах упорного подшипника
![]() . (2.12)
. (2.12)
Запишем дополнительные граничные условия, учитывающие случай поступления смазки в упорный подшипник при отсутствии в деформации упругого компонента
![]() .(2.13)
.(2.13)
Введем допущение, описывающее случай, когда смазочный материал, находясь в ненапряженном состоянии, подвергается внезапному сдвигу с заданной скоростью в момент подачи смазки в подшипник
![]() ,
,
откуда следует
![]() (2.14)
(2.14)
3. Точное автомодельное решение задачи 2.
Для системы дифференциальных уравнений (2.10) – (2.11), запишем в явном виде автомодельное решение с учетом граничных условий (2.12) – (2.14)
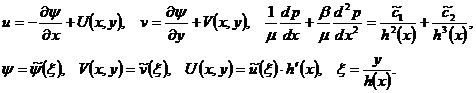 (2.15)
(2.15)
Подставим (2.15) в (2.10) и (2.11), получим
![]() , (2.16)
, (2.16)
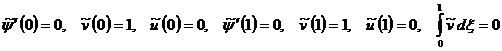 . (2.17)
. (2.17)
Решение системы уравнений (2.16) – (2.17) находится непосредственным интегрированием. В результате после необходимых исследований имеем:

где ![]() .
.
4 Определение гидродинамического давления в смазочном слое задача 2.
Для определения безразмерного гидродинамического давления в смазочном слое используем уравнение
![]() . (2.18)
. (2.18)
Введем обозначение
![]() . (2.19)
. (2.19)
С учетом (2.19) с точностью до членов ![]() уравнение (2.18) примет вид
уравнение (2.18) примет вид
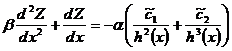 (2.20)
(2.20)
Решение системы (2.9), удовлетворяющее граничным условиям (2.12) и (2.13) можно записать в виде
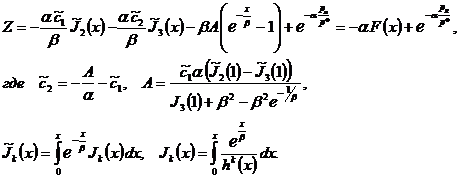 (2.21)
(2.21)
Воспользуемся аналитическими разложениями функций ![]() и
и ![]() . С точностью до членов
. С точностью до членов ![]() включительно получим алгебраическое уравнение для нахождения безразмерного параметра
включительно получим алгебраическое уравнение для нахождения безразмерного параметра ![]()
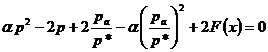 . (2.22)
. (2.22)
Решая уравнение (2.22), с точностью до членов ![]() ,
, 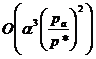 получим следующее выражение
получим следующее выражение
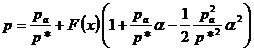 . (2.23)
. (2.23)
При вычислении интегралов, входящих в формулы (2.21), воспользуемся асимптотическим разложением функции ![]()
![]() .
.
С точностью до членов ![]() ,
, ![]() для
для ![]() после необходимых вычислений получим следующее выражение
после необходимых вычислений получим следующее выражение
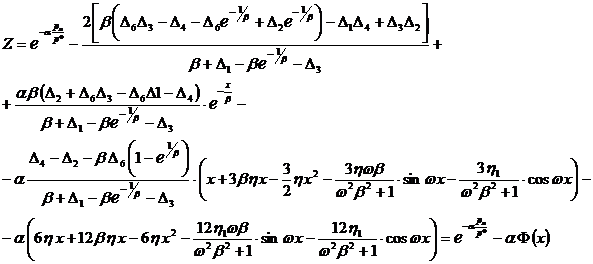 ,
,
(2.24)
где 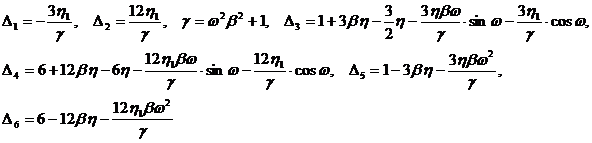 .
.
Для безразмерного гидродинамического давления в рассматриваемом случае получим выражение аналогичное (2.23)
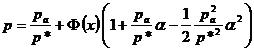 . (2.25)
. (2.25)
С учетом (2.25) для поддерживающей силы будем иметь
 . (2.26)
. (2.26)
Сила трения определяется выражением
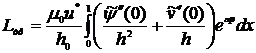 (2.27)
(2.27)
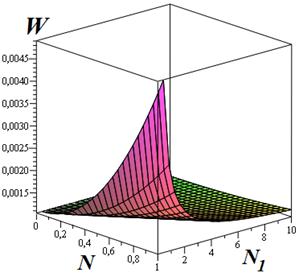
Результаты численного анализа, приведенные при различных значениях параметра ![]() , показывают, что:
, показывают, что:
1. В случае вязкоупругой смазки имеет место уменьшение несущей способности подшипника, работающего в стационарном режиме трения по сравнению с этим показателем для ньютоновской смазки.
2. В случае стационарного режима с увеличением значений параметра ![]() несущая способность резко уменьшается, при значении параметра
несущая способность резко уменьшается, при значении параметра ![]() несущая способность стабилизируется.
несущая способность стабилизируется.
3. С увеличением значений параметра ![]() несущая способность подшипника возрастает.
несущая способность подшипника возрастает.
4. При значении параметра ![]() близком к 0,5 рассматриваемый радиальный подшипник (по сравнению с
близком к 0,5 рассматриваемый радиальный подшипник (по сравнению с ![]() ) обладает свойством подшипника, так называемого, «двойного действия», по несущей способности.
) обладает свойством подшипника, так называемого, «двойного действия», по несущей способности.
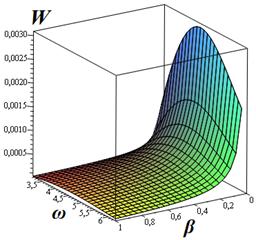
Рис. 2.1. Зависимость безразмерной несущей способности упорного подшипника от параметров ![]() и
и ![]() при учет зависимости вязкости от давления.
при учет зависимости вязкости от давления.
Литература:
1. Мигун, Н.П., Гидродинамика и теплообмен градиентных течений микроструктурной жидкости / Н.П. Прохоренко // Наука и техника. - 1984. – 264 с.
2. Типей, Н. Анализ смазки подшипников микрополярными жидкостями и его применение к коротким подшипникам / Н. Типей // Проблемы трения и смазки. – 1979. – № 3. – С. 122–131.
3. Allen, S. Y., Lubrication theory for micropolar fluids / S.Y. Allen, K.A. Kline// Trans. Asme, 1971. – V. E38. – No 4. – P. 646–656.
4. Вовк, А.Ю., Математическая модель прогнозирования значений безразмерных критериев микрополярной смазки, обеспечивающих рациональный режим работы упорного подшипника скольжения / А.Ю. Вовк, М.А. Савенкова// Труды РГУПС. – 2006. – № 2. – С. 29–34.
5. Ахвердиев, К.С., Математическая модель гидродинамической смазки бесконечно широких опор, работающих в турбулентном режиме на микрополярной смазке / К.С. Ахвердиев, А.Ю. Вовк, М.А. Мукутадзе, М.А. Савенкова // Трение и смазка в машинах и механизмах.– 2007.– № 9. – С. 12 –15.
6. Эркенов, А.Ч. Гидродинамический расчет радиального подшипника, близкого к круговому, работающего на микрополярной смазке / А.Ю. Вовк, И.С. Семенко, В.А. Константинов // Вестник РУПС. – 2009. – № 1. – С. 148–152.
7. Ахвердиев, К.С. Установившееся движение вязкоупругой жидкости между наклонным ползуном и направляющей с учетом сил инерции смазочной композиции / К.С. Ахвердиев, И.А. Журба // Трение и износ. –2004. – Т. 25. – №6. – С. 567-576.
8. Ахвердиев, К.С., Об устойчивости движения направляющей при неустановившемся течении вязкоупругой смазки в системе «ползун – направляющая» / К.С. Ахвердиев, И.А. Журба // Вестник РГУПС. – 2005.– №1. – С. 5–11.
9. Ахвердиев, К.С., Гидродинамический расчет подшипников скольжения с учетом сил инерции смазочной жидкости, обладающей вязкоупругими свойствами / К.С. Ахвердиев, М.В. Яковлев, И.А. Журба // Трение и износ.– 2003. – Т. 24. – №2. – С. 121–125.
10. Уилкок, Д.Ф. «Расчет упорных подшипников с эффективной работой в турбулентном режиме» /Д.Ф. Уилкок // Проблемы трения и смазки: Труды Американского общества инженеров-механиков. – 1977. – № 1. –С. 118–126.
11. Дерлугян Ф.П., Щербаков И.Н. Обоснование процесса получения композиционных антифрикционных самосмазывающихся материалов с заданными техническими характеристиками методом химического наноконструирования. [Электронный ресурс] // «Инженерный вестник Дона», 2010 г., №4 – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/287 (доступ свободный) – Загл. с экрана. – Яз. рус.
12. Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp Tower”s experiments / O. Reynolds. – Phil. Trans. Roy. Soc. London, 1886, vol. 177, pt. 1.
13. Мукутадзе М.А., Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки [Электронный ресурс] / Флек Б.М., Задорожная Н.С., Поляков Е.В., Мукутадзе А.М.// «Инженерный вестник Дона», 2013 г., №3 – Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/1765 (доступ свободный) – Загл. с экрана. – Яз. рус.