Идентификация математической модели главного золотника для системы диагностики и адаптивного управления открытием направляющего аппарата
Аннотация
Дата поступления статьи: 04.11.2013В статье рассмотрен процесс разработки алгоритма непрерывной идентификации математической модели главного золотника в реальном времени. Приведен квадратичный критерий качества обучения математической модели и синтез алгоритма непрерывной идентификации с помощью метода инвариантного погружения. Проведено компьютерное моделирование полученного алгоритма идентификации модели главного золотника с использованием реальных экспериментальных данных, полученных при пусках гидроагрегатов Волжской ГЭС. Результаты моделирования подтверждают эффективность разработанного алгоритма.
Ключевые слова: адаптивные системы управления, диагностика, электрогидравлические следящие системы, гидроагрегаты, золотник, рекуррентный метод наименьших квадратов, идентификация
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
05.13.05 - Элементы и устройства вычислительной техники и систем управления
На данный момент в гидроэнергетике широкое распространение получили гидроагрегаты с поворотно-лопастной турбиной. Главным регулирующим органом системы управления активной мощностью и частотой является система открытия направляющего аппарата [1]. Основными узлами системы открытия направляющего аппарата являются главный золотник и сервомотор. От качества и надежности работы данных узлов зависит качество работы гидроагрегата в целом.
Для повышения качества и надежности работы системы открытия направляющего аппарата была предложена адаптивная система управления и диагностики системы открытия направляющего аппарата [2]. Как известно, адаптивные системы управления являются эффективным инструментом повышения качества управления при изменяющихся условиях и наличии разного рода неопределенностей [3,4].
Важным этапом синтеза адаптивной системы управления является синтез математических моделей системы управления и алгоритма их идентификации в режиме реального времени [5].
Упрощенная схема главного золотника представлена на рис. 1. Золотник относится к классу регулируемых дросселирующих распределителей [6].
В качестве математической модели главного золотника были предложены нелинейная математическая модель и линейная модель с переменными параметрами. При достаточной скорости сходимости алгоритмов идентификации линейные модели с переменными параметрами эквивалентны моделям, линеаризованным вблизи опорной траектории [7]. Математическое моделирование показало, что линейная модель с переменными параметрами дает результаты по точности сравнимые с нелинейной моделью, поэтому для использования в контуре идентификации адаптивной системы управления была выбрана линейная математическая модель идентификации.
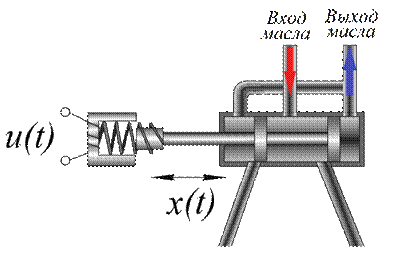
Рис. 1 – Упрощенная схема главного золотника системы открытия направляющего аппарата
В результате анализа сил, действующих на главный золотник, была получена следующая дискретная математическая модель главного золотника в пространстве состояний:
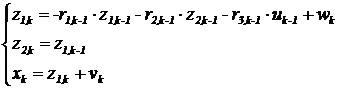
где zk=(z1,k z2,k)T=(xkxk-1)T – вектор переменных состояния главного золотника, xk – положение штока главного золотника в k-й момент времени, rk – вектор параметров математической модели главного золотника в k-й момент времени, подлежащие идентификации, wk. – неизвестное возмущающее воздействие, vk. – погрешность измерения.
Для идентификации переменных параметров математической модели главного золотника был составлен расширенный вектор переменных состояния и математическая модель главного золотника в расширенном пространстве состояния:
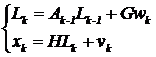
где ![]() - расширенный вектор переменных состояния,
- расширенный вектор переменных состояния, ![]() - матрицы коэффициентов:
- матрицы коэффициентов:
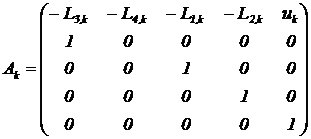 ,
,
![]() .
.
Таким образом, идентификация даже линейной системы приводит к нелинейным уравнениям состояния.
Идентификация системы подразумевает оценивание параметров этой системы оптимальное в смысле некоторого критерия идентификации или обучения. Таким образом, задача идентификации сводится к задаче оптимальной нелинейной фильтрации [8]. Также идентификацию можно трактовать как оптимальное управление объектом, описанным в расширенном пространстве состояний.
В зависимости от выбора критерия обучения могут получаться разные алгоритмы для идентификации одной и той же системы. Выбор критерия обучения является чаще всего интуитивным, эвристическим и зависит от предпочтений исследователя, так как нет единых правил для выбора «правильного» критерия [9]. Существуют различные критерии обучения, самыми распространенными из которых являются квадратичные, модульные и ступенчатые.
В качестве критерия обучения был принят квадратичный критерий:
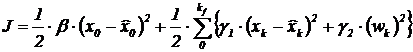 (1)
(1)
где ![]() - весовые коэффициенты,
- весовые коэффициенты, ![]() - оценка положения штока золотника по модели,
- оценка положения штока золотника по модели, ![]() - конечный момент времени оптимизационного процесса.
- конечный момент времени оптимизационного процесса.
Данный критерий совпадает с дискретным критерием максимума апостериорной вероятности (МАВ) при ![]() - дисперсия погрешности задания начальных условий,
- дисперсия погрешности задания начальных условий, ![]() и
и ![]() - дисперсии шумов процесса и шумов измерения, при этом шумы процесса считаются независимыми марковскими последовательностями гауссовских случайных величин с нулевым средним [10]. В таком случае данный метод дает наилучшие оценки в смысле байесовского максимума правдоподобия. Выполнение таких строгих условий в реальном процессе является практически невозможным. При невыполнении этих условий решение данной оптимизационной задачи с критерием гарантирует получение оценки оптимальной по методу наименьших квадратов [7,10].
- дисперсии шумов процесса и шумов измерения, при этом шумы процесса считаются независимыми марковскими последовательностями гауссовских случайных величин с нулевым средним [10]. В таком случае данный метод дает наилучшие оценки в смысле байесовского максимума правдоподобия. Выполнение таких строгих условий в реальном процессе является практически невозможным. При невыполнении этих условий решение данной оптимизационной задачи с критерием гарантирует получение оценки оптимальной по методу наименьших квадратов [7,10].
Таким образом, задача идентификации математической модели главного золотника сводится к минимизации выбранного критерия обучения (1) с ограничениями, задаваемыми математической моделью главного золотника.
Задачу можно решить с помощью дискретного принципа максимума Понтрягина или дискретных уравнений Эйлера-Лагранжа [10].. Гамильтониан для данной оптимизационной задачи:
![]()
где ![]() - вектор неопределенных множителей Лагранжа.
- вектор неопределенных множителей Лагранжа.
Канонические уравнения:
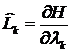 (2)
(2)
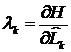 (3)
(3)
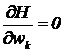 (4)
(4)
Граничные условия для канонических уравнений:
![]() (5)
(5)
![]() (6)
(6)
Каноническими уравнениями (2) – (4) и соответствующими граничными условиями (5), (6) определяется нелинейная двухточечная краевая задача (ДТКЗ), решением которой является искомый алгоритм оценки параметров системы [10].
Решение нелинейной ДТКЗ аналитически представляет собой чаще всего неразрешимую или очень сложную задачу, поэтому чаще всего ДТКЗ решаются численными методами.
Одним из возможных и эффективных методов решения ДТКЗ является метод инвариантного погружения. Основная идея метода инвариантного погружения состоит во включении частной задачи в более общую. Если можно решить общую задачу, то частная решается автоматически. Инвариантное погружение преобразует двухточечную краевую задачу к задаче Коши с заданными начальными условиями.
Метод инвариантного погружения является одним из самых мощных математических методов идентификации, позволяет оценивать состояние и параметры как линейных, так и нелинейных систем, а также позволяет проводить оценивание в контуре обратной связи реальных систем управления в оперативном текущем времени, т.е. пригоден для использования в адаптивных системах управления [11].
В данном случае осуществляется инвариантное погружение ДТКЗ (2) – (6), допустив, что условие на конце траектории при ![]() равно не нулю, а некоторому числу
равно не нулю, а некоторому числу ![]() . Кроме того, обобщается то, что величина
. Кроме того, обобщается то, что величина ![]() и момент времени
и момент времени ![]() переменны [7].
переменны [7].
В результате решения ДТКЗ (2) – (6) методом инвариантного погружения получается следующий алгоритм идентификации:
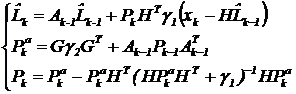
с начальными условиями
![]()

где ![]() - дисперсия оценивания переменных состояния,
- дисперсия оценивания переменных состояния, ![]() - дисперсия ошибки задания начальных условий для n-ой переменной состояния,
- дисперсия ошибки задания начальных условий для n-ой переменной состояния, ![]() - вспомогательная матрица (априорная дисперсия оценивания).
- вспомогательная матрица (априорная дисперсия оценивания).
Начальные оценки вектора параметров математической модели ![]() получены одношаговым методом наименьших квадратов.
получены одношаговым методом наименьших квадратов.
Для проверки адекватности математической модели было проведено компьютерное моделирование работы главного золотника системы открытия направляющего аппарата. Для моделирования использовались реальные значения управляющего сигнала и перемещения главного золотника, измеренные и записанные штатной системой управления во время пуска гидроагрегата № 2 Волжской ГЭС.
На рис. 2 представлен результат компьютерного моделирования процесса перемещения главного золотника системы открытия направляющего аппарата по линейной модели.
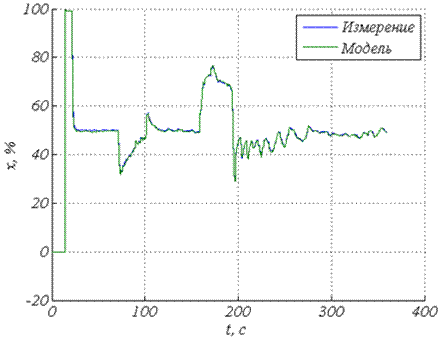
Рис. 2 – Моделирование перемещения главного золотника
На рис. 3 представлен сигнал невязки линейной модели и измеренных данных (ошибка моделирования).
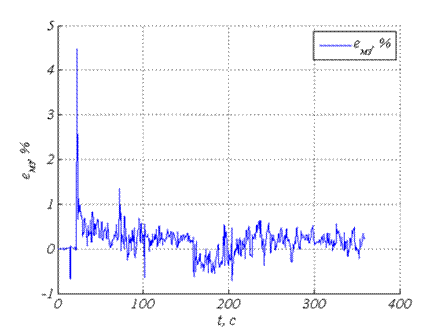
Рис. 3 – Сигнал невязки модели и измеренных данных
Среднее значение сигнала невязки ![]() , стандартное отклонение
, стандартное отклонение ![]() . Ошибка моделирования достигает максимального по модулю значения
. Ошибка моделирования достигает максимального по модулю значения ![]() в начальный момент времени во время пуска. Это связано с тем, что в начальный момент времени коэффициенты математической модели еще не подстроились. С течением времени невязка уменьшается.
в начальный момент времени во время пуска. Это связано с тем, что в начальный момент времени коэффициенты математической модели еще не подстроились. С течением времени невязка уменьшается.
Таким образом, получена линейная математическая модель главного золотника с переменными параметрами и алгоритм непрерывной идентификации параметров модели золотника. Результаты компьютерного моделирования с использованием реальных данных подтвердили адекватность линейной математической модели с переменными параметрами и эффективность алгоритма идентификации. Данная линейная математическая модель совместно с алгоритмом идентификации была использована для синтеза адаптивной системы управления открытием направляющего аппарата.
Литература
- Kjolle, A. Hydropower in Norway. Mechanical equipment / A. Kjolle. – Trondheim: NUST, 2001. – p. 183
- Браганец С.А., Гольцов А.С., Савчиц А.В. Система адаптивного управления и диагностики сервомоторов направляющего аппарата гидроагрегата с поворотно-лопастной турбиной [Электронный ресурс] // «Инженерный вестник Дона», 2013, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1807 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Н.А. Целигоров, Е.Н. Целигорова, Г.М. Мафура Математические модели неопределённостей систем управления и методы, используемые для их исследования [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1340 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Н.А. Целигоров, Г.М. Мафура Причины возникновения интервальных значений в математических моделях исследования робастной устойчивости систем управления [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p1y2012/1277 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Astrom K.J. Advanced PID control. –ISA. Triangle Park, 2006. – p. 446
- Схиртладзе, А.Г. В.Н. Гидравлические и пневматические системы [Текст]: Учебник для ВУЗов / А.Г. Схиртладзе, В.И. Иванов, В.Н. Кареев – М.: Высшая школа, 2006. – 534 с.
- Гольцов, А.С. Адаптивные системы: автоматическое управление нелинейными объектами: Монография / А.С. Гольцов. – Орел: Академия ФАПСИ, 2002. – 155 с.
- Красовский, А.А. Справочник по теории автоматического управления/ А. А. Красовский. – М.: Наука, 1987. –712 с.
- Цыпкин, Я. З. Информационная теория идентификации / Я.З. Цыпкин – М.: Наука, 1991. – 336 c.
- Сейдж, Э.П. Идентификация систем управления / Э.П. Сейдж, Д.П. Мелса – М.: Наука, 1974. – 248 c.
- Гроп Д. Методы идентификации систем / Д. Гроп – М.: Мир, 1979. – 302 c.