Математическое описание законов движения потока воздуха, свободно истекающего из камеры бытового холодильного прибора
Аннотация
Работа посвящена задаче математического описания свободного истечения потока охлажденного воздуха из камеры холодильника при открывании его дверей. Такие сведения необходимы для оценки объема замещения холодного воздуха теплым, в условиях эксплуатации морозильников и холодильников. Задача относится к разделу газодинамики и является относительно сложной, в виду наличия множества физических факторов, влияющих на процесс истечения холодного воздуха.
Прибегая к допущениям и перебирая различные подходы в математическом описании физических процессов, удалось составить замкнутую систему уравнений, описывающую процесс движения охлажденного потока воздуха.
Получена базовая система для нахождения скоростей потока при условии его ламинарности, что подтверждено экспериментальными исследованиями.
Ключевые слова: бытовой холодильник, движение холодного воздуха, энергосбережение, параметры потока.
Вопросы энергосбережения при эксплуатации бытовых холодильников являются актуальными, при этом важным является решение задачи снижения эксплуатационных потерь, обусловленных открыванием дверей холодильных и морозильных камер. Объем и скорость истечения охлажденного воздуха определяют дополнительные затраты энергии на охлаждение замещенного холодного воздуха теплым. Для оценки этих затрат необходимо составить математическую модель движения потока воздуха, свободно истекающего из камеры бытового холодильного прибора [1].
Рассматривается задача свободного истечения холодного воздуха из холодильной камеры при открывании дверей шкафа без учета влияния на поток внешних сил. Окружающий бытовой холодильник теплый воздух имеет меньшую плотность и холодный воздух движется из камеры вниз.
Рассмотрим общие закономерности, присущие рассматриваемой физической модели, описанные в [2]. В основу изучения движения вязкого газа положим следующие допущения.
1). Газ совершенен, т. е. давление «р», плотность «![]() » и абсолютная температура «Т» удовлетворяют уравнению состояния — закону Менделеева – Клапейрона:
» и абсолютная температура «Т» удовлетворяют уравнению состояния — закону Менделеева – Клапейрона:![]() (1)
(1)
где: ![]() универсальная газовая постоянная;
универсальная газовая постоянная;![]() молекулярная масса газа.
молекулярная масса газа.
2). Коэффициент удельной теплоемкости «![]() » не зависит от абсолютной температуры газа и является физической константой газа.
» не зависит от абсолютной температуры газа и является физической константой газа.
3). При истечении газа учитывается только вязкость первого рода (сопротивление окружающего теплого воздуха потоку холодного воздуха). Коэффициент теплопроводности газа «![]() » пропорционален коэффициенту динамической вязкости «
» пропорционален коэффициенту динамической вязкости «![]() », то есть выполняется критерий Прандтля:
», то есть выполняется критерий Прандтля:![]() (2)
(2)
4). К вышеописанным уравнениям присоединяется уравнение неразрывности движения: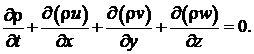 (3)
(3)
5). Газ представляет собой «ньютоновскую» среду, подчиненную известному обобщенному закону Ньютона о линейной связи между тензором напряжений и тензором скоростей деформаций.
Основные уравнения Навье — Стокса динамики вязкого газа, отнесенные к единице массы: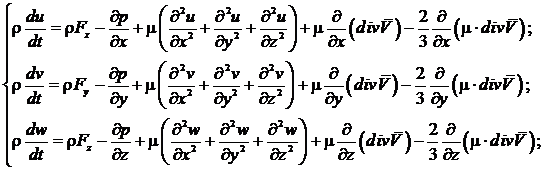 (4)
(4)
здесь: ![]() проекции вектора скорости
проекции вектора скорости ![]() на оси ОХ, ОУ, ОZ;
на оси ОХ, ОУ, ОZ;![]() вектор внешних объемных сил, действующих на газ в каждой точке пространства;
вектор внешних объемных сил, действующих на газ в каждой точке пространства;![]() коэффициент динамической вязкости;
коэффициент динамической вязкости;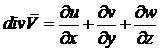 .
.
Полные производные ![]() можно представить в развернутой форме:
можно представить в развернутой форме: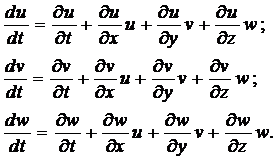 (5)
(5)
Полагаем, что внешние силы на воздушный поток внутри холодильника не влияют. Для данной модели можно рассмотреть допущение:![]() (6)
(6)
где ![]() ускорение силы тяжести.
ускорение силы тяжести.
При сформулированных выше допущениях система уравнений, описывающая истечение воздуха из холодильной камеры, содержит семь неизвестных функций: ![]() . В вышеописанной постановке задачи таких уравнений предложено шесть, в качестве седьмого уравнения для замыкания системы может быть предложено уравнение диффузии, либо уравнение теплового баланса.
. В вышеописанной постановке задачи таких уравнений предложено шесть, в качестве седьмого уравнения для замыкания системы может быть предложено уравнение диффузии, либо уравнение теплового баланса.
С формулируем граничные условия задачи.
1). Равенство нулю скорости на неподвижной твердой границе внутри холодильного шкафа.
2). Начальные скорости истечения холодного воздуха из шкафа равны нулю в каждой точке прямоугольного сечения на выходе из шкафа.
3). Задана температура воздуха внутри шкафа в начальный момент времени истечения холодного воздуха из шкафа и равна ![]() .
.
4). В начальный момент времени температура снаружи холодильного шкафа постоянна и равна ![]() .
.
5). Скорости воздушных масс снаружи холодильного агрегата в начальный момент открывания двери в каждой точке пространства равны нулю.
На первом этапе для упрощения задачи истечения холодного воздуха из холодильного шкафа будем дополнительно предполагать, что процесс истечения воздуха является изотермическим, то есть температура свободно истекающего потока воздуха постоянна в каждой точке потока истекающего воздуха. Такое условие означает, что исключается диффузионный процесс перемешивания холодного (свободно истекающего) воздуха и теплого (комнатного). Будем также предполагать, что вытекающий холодный воздух есть несжимаемая (нерасширяющаяся) среда.
При таких допущениях имеют место равенства:![]() (7)
(7)
Поскольку воздушный поток предполагается несжимаемым, то: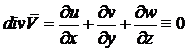 . (8)
. (8)
При сделанных допущениях уравнение неразрывности выполняется.
В силу условия (8) два последних слагаемых в каждом уравнении системы (4) равны нулю, учитывая формулы (1), (4) и допущения (6), (7), систему (5) преобразуем к более простому виду: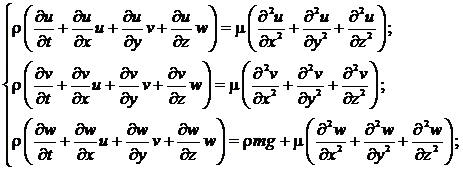 (9)
(9)
После сделанных допущений система (9) есть система трех уравнений относительно трех неизвестных функций ![]() , т. е. система (9) – замкнута.
, т. е. система (9) – замкнута.
Будем также полагать, что истечение холодного воздуха из шкафа происходит без изменения в горизонтальном поперечном направлении, т. е. что ординаты траекторий движения воздушных струй постоянны и изменение геометрии потока происходит только в плоскости XOZ (рис.1)

1 – верхнетемпературная камера;
2 – низкотемпературная камера.
Рис. 1 – Поведение свободно истекающего потока воздуха в плоскости XOZ
Предположение о неизменности геометрии потока в направлении оси OY влечет равенство нулю значений функции ![]() и функции
и функции ![]() , то есть они не зависят от переменной «
, то есть они не зависят от переменной «![]() ». Таким образом, реальный трехмерный поток заменяется моделью двухмерного.
». Таким образом, реальный трехмерный поток заменяется моделью двухмерного.
В этих условиях система (9) упростится: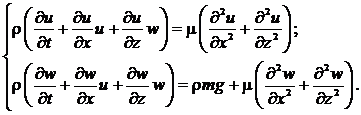 (10)
(10)
Будем дополнительно предполагать, что процесс истечения воздуха стационарный по времени, тогда: ![]() (11)
(11)
и система (10) упростится к виду: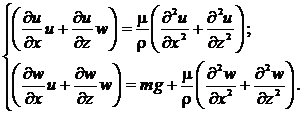 (12)
(12)
Так как система (12) содержит два уравнения и две неизвестные функции, то она является замкнутой.
Систему (12) можно классифицировать, как систему двух нелинейных дифференциальных уравнений в частных производных второго порядка. В настоящее время в технической литературе методы решения таких задач неизвестны. В данной работе систему (12) предлагается решать приближенными аналитическими методами.
Выражения 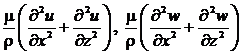 , входящие в оба уравнения системы (12), определяют силы аэродинамического сопротивления воздушной среды комнаты, которая тормозит холодный воздушный поток, истекающий из холодильной камеры.
, входящие в оба уравнения системы (12), определяют силы аэродинамического сопротивления воздушной среды комнаты, которая тормозит холодный воздушный поток, истекающий из холодильной камеры.
Систему уравнений (12) будем преобразовывать исходя из того, что в технической аэродинамике силу сопротивления воздушной среды приближенно определяют по формулам (в так называемой зоне квадратичного сопротивления):
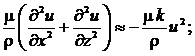 (13)
(13)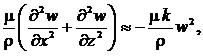
здесь ![]() коэффициент пропорциональности, определяемый экспериментально.
коэффициент пропорциональности, определяемый экспериментально.
Так как коэффициент динамической вязкости ![]() имеет единицы измерения
имеет единицы измерения ![]() , то из уравнений (13) получаем, что
, то из уравнений (13) получаем, что ![]() измеряется в
измеряется в ![]() .
.
Знак минус в правых частях равенств (13) указывает на то, что вторые частные производные от проекций вектора скорости отрицательны из-за тормозящего влияния вязкой среды.
В силу формул (13) система (12) преобразуется к виду:
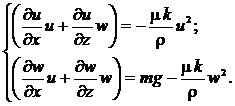 (14)
(14)
Система (14) является базовой для нахождения скоростей ламинарного потока при его свободном истечении из холодильной камеры в стационарном режиме.
Литература.
- 1. Левкин, В.В. Тепловые расчеты сборочных единиц бытовых холодильников / В.В. Левкин. Шахты.: АП «Полиграфист», 1994. – 229 с.
2. Лойцянский, Л.Г. Механика жидкости и газа / Л.Г. Лойцянский. – 5-е изд. – М.: Наука, 1978. – 736 с.
3. Корн, Г. Справочник по математике для научных работников и инженеров/ Г. Корн, Т. Корн. – М.: Наука, 1970. – 720 с.