Погонная индуктивность витой пары на сверхвысоких частотах
Аннотация
Предложен подход для расчета погонной индуктивности витой пары на сверхвысоких частотах. Приведены аналитические соотношения для расчета погонной индуктивности двухпроводной линии и витой пары на СВЧ. Предложен эффективный алгоритм приближенного расчета погонной индуктивности витой пары при любом угле наклона жилы.
Ключевые слова: погонная индуктивность, сверхвысокие частоты, витая пара, двухпроводная линия, угол наклона жилы
Известно, что сверхвысокочастотное электромагнитное поле практически не проникает внутрь проводников, и электрический ток распределяется в весьма тонком слое по их поверхности. Толщина этого, так называемого, скин-слоя D° определяется соотношением [1]
![]() ,
,
где f – частота (Гц), µ0=4π×10-7 (Гн/м) – магнитная постоянная, σ (См/м) - удельная электропроводность провода. Например, на частоте f=3 ГГц в медных проводниках с удельной проводимостью σ=5.88×107 См/м толщина скин-слоя составляет всего Δ°≈2.9 мкм, что, например, в 170 раз меньше радиуса провода миллиметрового диаметра.
Характер распределения тока в проводниках длинной линии определяется не только скин-эффектом, но и эффектом близости проводников. Поэтому распределение тока по поверхности проводников длинной линии (и витой пары) зависит от конфигурации ее поперечного сечения. Поверхностная плотность тока равна касательной к поверхности составляющей напряженности магнитного поля, т.к. определяется соотношением
![]() ,
,
где ![]() - орт внешней нормали к поверхности проводника, как показано на рис.1.
- орт внешней нормали к поверхности проводника, как показано на рис.1.
Итак, чтобы найти поверхностную плотность тока в любой точке поверхности проводника, надо знать![]() в этой точке. Воспользуемся первым типом соответствия электростатического и магнитного полей [2], при котором картина магнитных силовых линий рассматриваемой системы совпадает с картиной ее электростатических эквипотенциалей, а картина магнитных эквипотенциалей совпадает с картиной электрических силовых линий. Исходя из этого соответствия, можно внешнее, по отношению к проводам, магнитное поле двухпроводной линии представить как магнитное поле двух линейных токов, смещенных от оси проводников [3] на расстояние
в этой точке. Воспользуемся первым типом соответствия электростатического и магнитного полей [2], при котором картина магнитных силовых линий рассматриваемой системы совпадает с картиной ее электростатических эквипотенциалей, а картина магнитных эквипотенциалей совпадает с картиной электрических силовых линий. Исходя из этого соответствия, можно внешнее, по отношению к проводам, магнитное поле двухпроводной линии представить как магнитное поле двух линейных токов, смещенных от оси проводников [3] на расстояние![]() (см. рис. 1).
(см. рис. 1).
Напряженность магнитного поля в произвольной точке m(R,φ) поверхности правого проводника линии можно записать в виде суперпозиции полей двух бесконечно длинных нитей тока I, т.е.
![]()
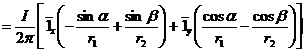 где
где![]()
.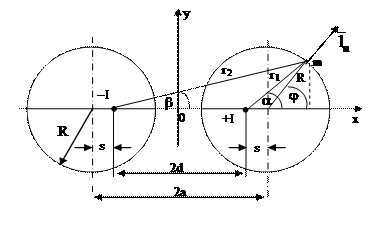
Рис.1. - К расчету магнитного поля двухпроводной линии
Следовательно,
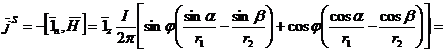
![]()
где ![]()
![]() .
.
Результаты расчета распределения продольного поверхностного тока по верхней полуокружности правого проводника (см. рис. 1) представлены на рис. 2. Картина распределения тока по нижней полуокружности симметрична. Абсолютные значения ![]() на рис. 2 приведены для R=0.5мм=0.0005м и силы тока в линии I=1 А. Интеграл от
на рис. 2 приведены для R=0.5мм=0.0005м и силы тока в линии I=1 А. Интеграл от ![]() по периметру провода при любом R/a дает один и тот же результат – силу тока в проводе (в нашем случае I=1А).
по периметру провода при любом R/a дает один и тот же результат – силу тока в проводе (в нашем случае I=1А).
Погонная индуктивность двухпроводной линии на СВЧ. Определение погонной индуктивности при неравномерном распределении тока удается произвести далеко не всегда. Как правило, это можно сделать при ярко выраженном скин-эффекте, когда ток распределен строго по поверхности проводников, а его распределение известно, например, оно определяется эффектом близости проводов кругового сечения, как в нашем случае.
Рассмотрим для начала бесконечно длинную двухпроводную линию. Выделим две нити тока di’ и di”, как показано на рис. 3. Векторный потенциал, создаваемый током di’ в любой точке нити di”, равен
![]()
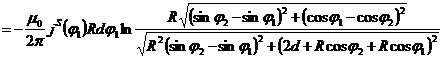 ,
,
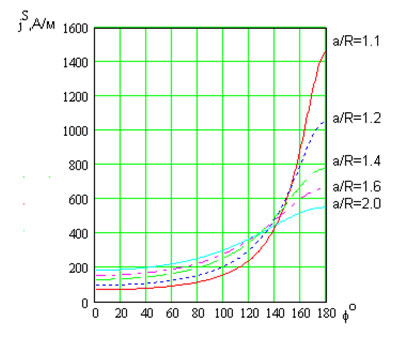
Рис. 2. - Результаты расчета распределения продольного поверхностного тока по верхней полуокружности правого проводника
а потенциал, создаваемый всеми поверхностными токами на данной нити тока, соответственно
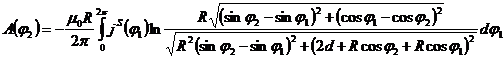 .
.
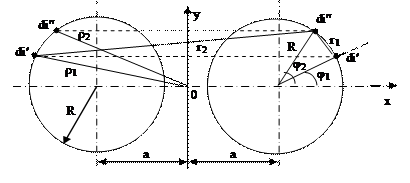
Рис. 3. - К расчету бесконечно длинной двухпроводной линии
Потенциал A(φ2) обеспечивает потокосцепление только с di”, нитью тока. Чтобы определить полное потокосцепление нитей di’ и di”, на участке l линии, функцию необходимо умножить на 2l, т.к. нить di”, имеет прямой и обратный участок. Полученный результат необходимо проинтегрировать по всем нитям тока di”,. Наконец, чтобы найти погонную индуктивность ![]() линии, полученную выше функцию
линии, полученную выше функцию![]() надо разделить на длину участка l и квадрат силы тока в линии и вычислить интеграл
надо разделить на длину участка l и квадрат силы тока в линии и вычислить интеграл
![]()
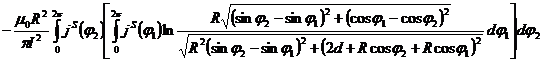 . (1)
. (1)
Здесь
![]()
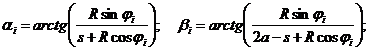
![]()
![]()
Сравним расчетные данные ![]() , полученные с помощью справочной формулы [4]:
, полученные с помощью справочной формулы [4]:
![]() (2)
(2)
для двухпроводной линии при весьма высокой частоте с результатом численного интегрирования (1). Рис. 4 иллюстрирует почти идеальное совпадение результатов (рис. 4,а): ошибка ![]() не превышает 0.07% в диапазоне изменения 1.05‹a/R‹4/0. Численное интегрирование проведено в среде MathCAD 2001.
не превышает 0.07% в диапазоне изменения 1.05‹a/R‹4/0. Численное интегрирование проведено в среде MathCAD 2001.
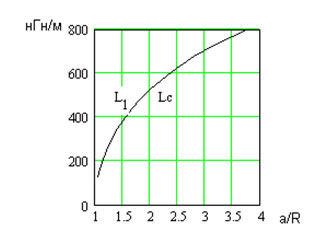
Рис. 4. - Сравнение результатов расчета по справочной формуле с результатами численного интегрирования
Погонная индуктивность витой пары на СВЧ. Строго говоря, погонную индуктивность витой пары L1S можно определить, зная угол наклона жилы β и параметры поперечного сечения пары a,R. Для этого необходимо вычислить интеграл
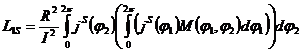 , (3)
, (3)
в котором [5]
![]()
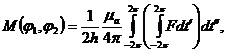 (4)
(4)
где h – шаг витой пары, а функция
![]()
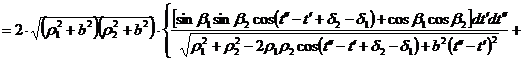
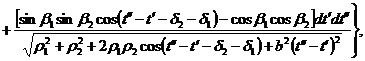
Здесь при вычислении взаимной индуктивности (4) двух выделенных нитей с целью увеличения точности результатов функцию![]() интегрируем в пределах не одного, а двух шагов витой пары. Геометрия сечения пары плоскостью z=0 приведена на рис. 5.
интегрируем в пределах не одного, а двух шагов витой пары. Геометрия сечения пары плоскостью z=0 приведена на рис. 5.
При вычислении интегралов используются следующие обозначения [5]:
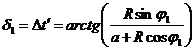 ; ,
; ,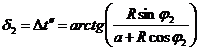
![]() ;
; ![]() .
.
![]() ;
; ![]()
![]() ;
;![]()
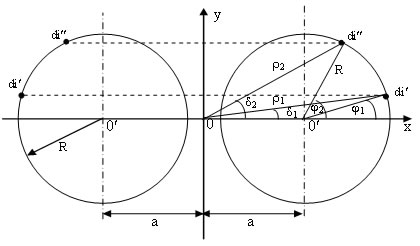
Рис. 5. - К расчету взаимной индуктивности двух выделенных нитей
Для вычисления интегралов (3) и (4) необходимы специальные программы, разработка которых требует дополнительных затрат сил и времени. В то же время можно предложить способ приближенного расчета погонной индуктивности, аналогичный способу, предложенному в [6]. При расчете погонной индуктивности витой пары на весьма высоких частотах тоже можно использовать принцип средних геометрических расстояний, и, как показывают расчеты, результаты имеют хорошее совпадение при a/R>3.0. При этом эквидистантные нити тока должны смещаться относительно геометрических осей проводников на расстояние
![]() ,
,
а средним геометрическим расстоянием [4] поверхностно распределенных токов будет![]() .
.
Сравним взаимные погонные индуктивности одинаковых эквидистантных пар нитей поверхностного тока в длинной линии Ml и в аналогичной витой паре Ms при малом угле наклона жилы (b=2°). Абсолютные значения Ms приведены на рис. 6,а, а их относительное отличие от Ml ( ![]() %) - на рис. 6,б.
%) - на рис. 6,б.
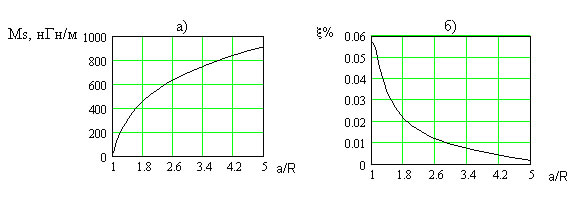
Рис. 6. - Результаты расчета взаимных погонных индуктивностей (а); их относительное отличие от Ml ( ![]() %) (б).
%) (б).
Итак, для эквидистантных нитей тока Ms практически идеально совпадает с Ml при любых значениях a/R (ошибка не превышает 0.06% и объясняется, скорее всего, погрешностью численного интегрирования). Такой результат позволяет предложить следующий алгоритм приближенного расчета погонной индуктивности витой пары при любом угле наклона жилы:
![]() ,
,
где Lc – справочное значение погонной индуктивности прямой длинной линии (3) при весьма высокой частоте [4], а
![]()
- корректирующая функция. Расчет корректирующей функции для эквидистантных нитей проведен в среде MathCAD 2001, а его результаты представлены в табл. 1 и иллюстрируются кривыми рис. 7.
Таблица № 1
Корректирующая функция f(a/R,β)
|
β° |
a/R |
||||||||
|
1.1 |
1.2 |
1.4 |
1.6 |
1.8 |
2.0 |
2.5 |
3.0 |
3.5 |
|
|
2 |
0.999455 |
0.999547 |
0.999669 |
0.999705 |
0.999788 |
0.999819 |
0.999876 |
0.999909 |
0.999933 |
|
4 |
1.001831 |
1.002222 |
1.002648 |
1.002848 |
1.002845 |
1.002989 |
1.003002 |
1.002971 |
1.002932 |
|
6 |
1.006136 |
1.006959 |
1.007930 |
1.008218 |
1.008391 |
1.008454 |
1.008410 |
1.008281 |
1.008142 |
|
8 |
1.011850 |
1.013239 |
1.014700 |
1.015351 |
1.015633 |
1.015731 |
1.015636 |
1.015408 |
1.015157 |
|
10 |
1.018760 |
1.020770 |
1.022938 |
1.023916 |
1.024353 |
1.024518 |
1.024425 |
1.024098 |
1.023739 |
|
12 |
1.026580 |
1.029358 |
1.032342 |
1.033723 |
1.034355 |
1.034627 |
1.034580 |
1.034190 |
1.033735 |
|
14 |
1.035254 |
1.038852 |
1.042778 |
1.044649 |
1.045539 |
1.045911 |
1.045999 |
1.045578 |
1.045056 |
|
16 |
1.044680 |
1.049186 |
1.054174 |
1.056590 |
1.057808 |
1.058385 |
1.058620 |
1.058211 |
1.057643 |
|
18 |
1.054811 |
1.060312 |
1.066472 |
1.069527 |
1.071113 |
1.071930 |
1.072414 |
1.072065 |
1.071484 |
|
20 |
1.065817 |
1.072196 |
1.079858 |
1.083438 |
1.085465 |
1.086554 |
1.087383 |
1.087148 |
1.086590 |
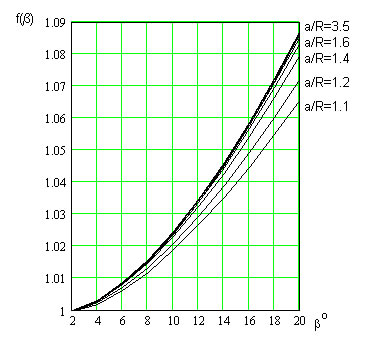
Рис. 7. - Корректирующая функция для эквидистантных нитей
Выводы:
1. Для витой пары любого поперечного сечения погонная индуктивность больше погонной индуктивности прямой линии такого же поперечного размера и при заданном a/R отличается тем больше, чем больше угол наклона жилы β.
2. Это отличие тем больше, чем больше a/R: например, при β=20о витая пара с a/R=3.0 имеет погонную индуктивность на 8.7% больше чем соответствующая прямая линия, а при a/R=1.1 – только на 6.6%.
Результаты исследований изложенные в данной статье получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта "Создание высокотехнологичного производства по изготовлению информационно-телекоммуникационных комплексов спутниковой навигации ГЛОНАСС/GPS/Galileo" по постановлению правительства №218 от 09.04.2010 г.
Литература
- Рамо С., Уиннери Дж. Поля и волны в современной радиотехнике. [Текст] / Пер. с англ. // Под ред. Ю.Б. Кобзева. – М: Мир. - 1960 г.
- Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. [Текст] / М: Высшая школа. 1978 г.
- Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. [Текст] / М: «Сов. радио». – 1971 г.
- Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. [Текст] / Справочная книга. – Л: Энергия. - 1970 г. - 416 с.