Способ кодирования чисел ДНК-цепочками и основные операции для выполнения арифметических действий в парадигме ДНК-вычисления

Аннотация

А.Ю. Клепиков, В.С. Ростовцев

Рассматривается способ кодирования чисел, представленных в различных системах счисления, ДНК-цепочками, а также приведён минимальный необходимый набор операций над ДНК для выполнения арифметических операций. Предложенный способ кодирования и операции над ДНК по сравнению с известными моделями ДНК-вычислений позволяют увеличить скорость выполнения арифметических операций, повысить точность вычислений, выполнять операции над числами как с фиксированной запятой, так и с плавающей.

Ключевые слова: кодирование чисел, ДНК-цепочки, операции с ДНК-цепочками, ДНК-вычисления

05.13.15 - Вычислительные машины, комплексы и компьютерные сети

Одним из направлений исследования в области выполнения вычислений, основанных на парадигме использования принципов взаимодействия дезоксирибонуклеиновой кислоты (ДНК), является разработка способов кодирования чисел и выполнения арифметических операций над ними. Существует несколько моделей ДНК-вычислений [1], но наибольшее распространение получили две из них: модель, основанная на самосборке (self-assembly) ДНК, и модель, основанная на RDNA.
Модель, основанная на самосборке (self-assembly) ДНК [2, 3], является более гибкой для вычислений, но даёт замедление при моделировании. При ускорении процесса выполнения операций, в геометрической прогрессии возрастает частота появления ошибок и сам процесс выходит из-под контроля [1]. Модель, основанная на RDNA [4, 5], является более простой. Она меньше подвержена ошибкам, но и менее гибкая, чем модель, основанная на самосборке [1].
В перечисленных моделях каждое число, участвующее в арифметической операции, сначала переводится в двоичную систему счисления, а затем каждый бит числа кодируется цепочкой нуклеотидов. Такой способ приводит к появлению ошибок вычисления уже на этапе кодирования, а также к использованию ДНК-цепочек большой длины. При этом для выполнения арифметических операций могут использоваться только числа с фиксированной запятой.
Авторами предлагается улучшить модель, приведённую в работах [4, 5]. Для этого предлагается изменить способ кодирования чисел и определить необходимые операции над ДНК-цепочками. В этой статье предложен способ однозначного сопоставления ДНК-кодов и чисел, представленных в другой системе счисления, например восьмеричной, двенадцатеричной и т.п. Кроме того, представлен минимальный набор операций над ДНК-цепочками, необходимый для выполнения арифметических операций.
1. Модель ДНК-вычисления
Ключевым компонентом ДНК-вычислений является набор ДНК-цепочек. Одиночную цепочку ДНК можно определить как строку, состоящую из нуклеотидов: аденин (А, A), тимин/урацил (Т/У, T/U), гуанин (Г, G), цитозин (Ц, C). Любую одиночную цепочку можно синтезировать, используя биологические методы [6]. Каждая цепочка имеет одно из двух направлений: прямое (5'-3') или обратное (3'-5'). Например, прямое направление 5'-AATG, обратное направление этой же цепочки 3'-GTAA.
В основе ДНК-вычислений лежит принцип комплементарности Уотсона-Крика (Watson-Crick complementarity). Под комплементарностью понимается строгое взаимное соответствие соединения нуклеотидов, в котором: А-Т (аденин соединяется с тимином), Г-Ц (гуанин соединяется с цитозином). Двойная ДНК-цепочка образуется из двух одинарных цепочек только в том случае, если каждый нуклеотид одной цепочки является комплементарным соответствующему нуклеотиду второй цепочки [1].
Определены основные операции,  основанные на модели ДНК-вычислений и  используемые при выполнении арифметических операций:

1. ДЕНАТУРАЦИЯ (T). Дана пробирка T, содержащая двойные цепочки ДНК. Результатом выполнения операции ДЕНАТУРАЦИЯ (T) будет пробирка T с одинарными ДНК-цепочками, которые образовались путем разделения всех двойных цепочек в T на одинарные, 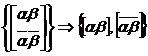, где α и β – нуклеотидные последовательности, 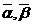- соответствующие комплементарные нуклеотидные последовательности.
2. ОПРЕДЕЛИТЬ (T). Дана пробирка T. Результатом выполнения операции ОПРЕДЕЛИТЬ (T) будет истинное значение, если в пробирке T содержится хотя бы одна цепочка ДНК, в противном случае – ложное значение.
3. ОЧИСТИТЬ (T). Дана пробирка T, содержащая цепочки ДНК. Результатом выполнения операции ОЧИСТИТЬ (T) будет пустая пробирка T.
4. РАЗДЕЛИТЬ (T₁, X, T₂). Дана пробирка T₁ с ДНК-цепочками и набор строк (ДНК-цепочек) X. После выполнения операции РАЗДЕЛИТЬ (T₁, X, T₂) будут выбраны все цепочки из T₁, содержащие строку из множества X, и помещены в пробирку T₂.
5. РАЗРЕЗАТЬ (T₁, q). Дана пробирка T₁ и строка (ДНК-цепочка) q. После выполнения операции РАЗРЕЗАТЬ (T₁, q) будут разрезаны все ДНК-цепочки в пробирке T₁, содержащие строку q, до строки q. .
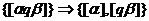6. РАЗРЕЗАТЬ (q, T₁). Дана пробирка T₁ и строка (ДНК-цепочка) q. После выполнения операции РАЗРЕЗАТЬ (q, T₁,) будут разрезаны все ДНК-цепочки в пробирке T₁, содержащие строку q, после строки q. .
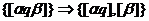7. РЕНАТУРАЦИЯ (T). Дана пробирка T, содержащая одинарные цепочки ДНК. Результатом выполнения операции РЕНАТУРАЦИЯ (T) будет пробирка T со всеми возможными двойными ДНК-цепочками, которые образовались.
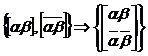
8. СЛИТЬ (T₁, T₂). Даны две пробирки с содержащимися в них цепочками ДНК. После выполнения операции СЛИТЬ (T₁, T₂) в пробирке T₂ будут находиться ДНК-цепочки из T₁ и T₂. .
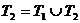9. СОЕДИНИТЬ (T, q). Дана пробирка T, содержащая ДНК-цепочки, и строка (ДНК-цепочка) q. Результатом выполнения операции СОЕДИНИТЬ (T, q) будет пробирка T с цепочками ДНК, к концу каждой из которых присоединены строки q.

2. Способ кодирования чисел ДНК-цепочками
Предлагается способ кодирования n-разрядных чисел с помощью ДНК-цепочек, представленных в некоторой системе счисления.
При выполнении арифметических операций участвуют два числа. Каждое n-разрядное число кодируется несколькими параметрами, состоящими из номера разряда и значения разряда.
Каждый параметр n-разрядного первого числа кодируется следующим образом:
 ,
где d_i – i разряд числа; S_i – закодированный ДНК-цепочкой номер разряда числа; K_i – закодированное ДНК-цепочкой значение разряда числа; дефис используется только для улучшения наглядности представления. Таким образом, каждый разряд первого числа состоит из номера разряда и значения этого разряда, закодированные ДНК-цепочками.
Каждый разряд n-разрядного второго числа кодируется следующим образом:
 ,
где d_i – i разряд числа;  – комплементарная цепочка закодированного ДНК-цепочкой номера разряда числа в обратном направлении; K_i – закодированное ДНК-цепочкой значение разряда числа. Таким образом, второе число состоит из значения разряда числа и комплементарного номера разряда в обратном направлении, закодированные ДНК-цепочками.
Количество нуклеотидов для кодирования значений разрядов определяется следующим образом:
,
где I – необходимое количество нуклеотидов для кодирования разрядов числа; b – основание системы счисления.
Цифры в b-ричной системе счисления кодируются следующим образом: цифры, дополняющие друг друга, кодируются комплементарными ДНК-цепочками.
Номер разряда числа кодируется уникальным набором нуклеотидов, полностью не совпадающим с используемой кодировкой разрядов числа. Количество нуклеотидов выбирается в зависимости от числа разрядов.
Любая арифметическая операция выполняется над двумя числами, закодированными ДНК-цепочками, каждое из которых помещают в отдельную пробирку. Кроме операндов, в предлагаемом способе используются частичные суммы, закодированные ДНК-цепочками. Предполагается, что они помещены в пробирку частичных сумм. Данные значения получаются путем суммирования всех возможных вариантов цифр b-ричной системы счисления. ДНК-цепочки в пробирке частичных сумм кодируют следующим образом:
 ,
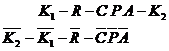где K₁ – закодированный ДНК-цепочкой разряд n-разрядного первого слагаемого; K₂ – закодированный ДНК-цепочкой разряд n-разрядного второго слагаемого;  – закодированный комплементарной ДНК-цепочкой разряд n-разрядного первого слагаемого;  – закодированный комплементарной ДНК-цепочкой разряд n-разрядного второго слагаемого; R – закодированный ДНК-цепочкой разделитель частичной суммы;  – комплементарная цепочка разделителя частичной суммы; C – закодированная ДНК-цепочкой единица переноса (если имеется);  – комплементарная ДНК-цепочка единицы переноса; P – закодированный ДНК-цепочкой разделитель результирующей части и переноса (если имеется единица переноса);  – комплементарная цепочка разделителя P; A – закодированный ДНК-цепочкой результат суммы двух разрядов K₁ и K₂;  – комплементарная цепочка суммы A; дефис используется только для улучшения наглядности представления.
Разделители R и P кодируются уникальными минимальными наборами нуклеотидов, не совпадающими полностью с используемой кодировкой разрядов числа. Количество нуклеотидов выбирается в зависимости от числа разрядов.
3. Пример кодирования восьмеричной системы счисления
Для восьмеричной системы счисления при кодировании цифр требуется использовать две нуклеотидные последовательности. В таблице 1 представлено кодирование цифр восьмеричной системы счисления с помощью ДНК-цепочек.

Таблица № 1
Кодирование цифр восьмеричной системы счисления

Количество частичных сумм в восьмеричной системе счисления может быть 64. В таблицах 2 - 4 представлено кодирование частичных сумм. Для большей наглядности закодированные разделители частичной суммы, а также результирующей части и переноса показаны символами R и P соответственно. Они могут быть закодированы неиспользуемыми при кодировании цифр восьмеричной системы счисления нуклеотидными последовательностями AG и AC.
Таблица № 2
Кодирование частичных сумм восьмеричной системы счисления

Например, число пять, представленное в восьмеричной системе счисления, состоит из одного разряда. Оно будет закодировано с помощью ДНК-цепочек следующим образом: S₀ – TT.
При этом номер разряда S₀ может быть закодирован либо нуклеотидной последовательностью GG (закодированная с помощью ДНК цифра ноль); либо любой последовательностью одинаковых нуклеотидов (в данном случае одинарным нуклеотидом), отделенных уникальным набором нуклеотидов; либо какой-либо другой уникальной последовательностью нуклеотидов.
Таблица № 3
Кодирование частичных сумм восьмеричной системы счисления

Таблица № 4
Кодирование частичных сумм восьмеричной системы счисления

При выполнении арифметических операций используется четыре пробирки [7]; по одной пробирке для каждого из двух участвующих в операции чисел, одна пробирка для частичных сумм и одна пробирка используется в качестве буфера. В пробирке с частичными суммами числа кодируется один раз до начала выполнения арифметических операций.
Любая арифметическая операция с числами, представленными кодами ДНК, может быть выполнена с помощью перечисленных выше девяти операций над ДНК-цепочками. Такой набор является минимально необходимым.

Заключение
Предложенный способ кодирования чисел ДНК-цепочками позволяет представлять числа не только с фиксированной запятой, как в известных моделях, но и с плавающей запятой.
Однозначное сопоставление кода ДНК с цифрой выбранной системы счисления без использования промежуточных преобразований позволяет при кодировании повысить точность дальнейших арифметических вычислений. Это объясняется тем, что не требуется обязательного перевода числа в двоичную систему счисления. Данный способ предоставляет возможность представлять и обрабатывать числа, закодированные в различных системах счисления.
Такое кодирование позволяет использовать меньшее количество нуклеотидов для представления разрядов чисел по сравнению с известными моделями, где количество зависит от конкретного кодируемого разряда числа. Это значит, что длина ДНК-цепочки каждого числа меньше, а при больших числах значительно меньше. Это преимущество уменьшает количество ошибок, возникающих при образовании кодирующей ДНК. Также становится более простым и быстрым процесс выполнения операций.
Применение данного способа также позволяет сократить временные затраты на представление чисел в виде цепочек ДНК. Это связано с тем, что скорость формирования нуклеотидной последовательности напрямую зависит от её длины. А также сокращение временных затрат связано с исключением промежуточного кодирования в двоичную систему счисления.
Авторами предложен минимально необходимый набор операций над ДНК-цепочками для выполнения арифметических операций. Количество предложенных операций меньше, чем в известных моделях. Это позволяет сократить накладные расходы.

Литература

1. Zhiquan Frank Qiu Advance the DNA computing: dissertation PhD 2003. 75 p.
2. Robert Barish, Paul Rothemund, Erik Winfree Two computational primitives for algorithmic self-assembly: Copying and counting // Nano Letters, 5 (12), 2005. pp. 2586-2592.
3. Yuriy Brun, Arithmetic computation in the tile assembly model: Addition and multiplication, Theoretical Computer Science, vol. 378, no. 1, June 2007, pp. 17–31.
4. Rana Barua, Jonardan Misra Binary Arithmetic for DNA Computers // DNA Computing: 8th International Workshop on DNA Based Computers, DNA8, Sapporo, Japan, June 10-13, 2002, Revised Papers. – Springer-Verlag: London, UK, 2003. – pp. 124-132.
5. Akihiro Fujiwara, Matsumoto K., Wei Chen Addressable procedures for logic and arithmetic operations with DNA strands // International Parallel and Distributed Processing Symposium, Nice, France, 22-26 April 2003.
6. Паун, Г. ДНК-компьютер. Новая парадигма вычислений. [Текст] / Паун Г., Розенберг Г., Саломаа А.; под ред. М.В. Волкова. – Москва: Мир, 2003 - 528 с.
7. Способ моделирования процесса суммирования положительных n-разрядных чисел, закодированных ДНК-цепочками / Ростовцев В.С., Клепиков А.Ю.; приоритетное уведомление рег. номер 2012142920  приоритет 08.10.2012.