Сравнение сдвига совокупности конечного объема и минимального выборочного значения в зависимости от параметров моделирования для деталей экскаватора
Аннотация
Производится сравнение сдвига совокупности конечного объема и минимального выборочного значения в зависимости от параметров моделирования для деталей экскаватора. В результате проведенных исследований выявлена следующая закономерность: в интервале размахов совокупностей R=17-20 все коэффициенты значительно отличаются от значений других размахов.
Ключевые слова: Генеральная совокупность конечного объема, размах совокупности, сдвиг совокупности, минимальное выборочное значение, выборка.
В машиностроительной отрасли большое значение уделяют надежности строительных машин в частности экскаваторов. В теории и практике надежности в качестве статистического материала используют исходные данные выборок, объем которых обычно составляет n=10-100. Вместе с тем объем эксплуатируемых машин может составлять тысячи или даже миллионы, образуя генеральную совокупность конечного объема. Поэтому в расчетах необходимо переходить от выборочных данных к данным генеральной совокупности конечного объема. Для этого используют аналитический и корреляционный методы. В статье [1] принято равенство сдвигов крайних членов Скч выборок и совокупности конечного объема Сс с ошибкой 3-5%. Но на практике сдвиг является абстрактной величиной, поэтому принято решение о проведении анализа сдвига совокупности Сс и минимального значения выборки x1.
Проведен анализ параметра Сс совокупности конечного объема относительно минимального значения-х1 выборок из совокупности (рис.1).
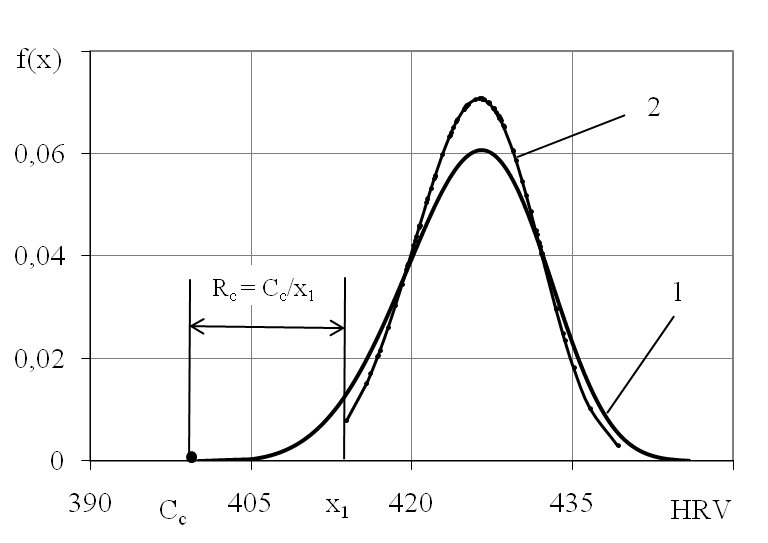
Рис.1. График плотности распределения: 1-совокупность; 2- выборка
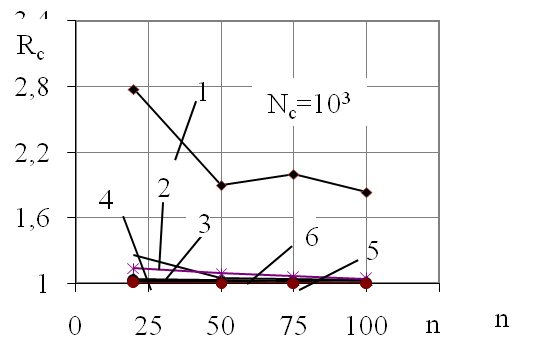
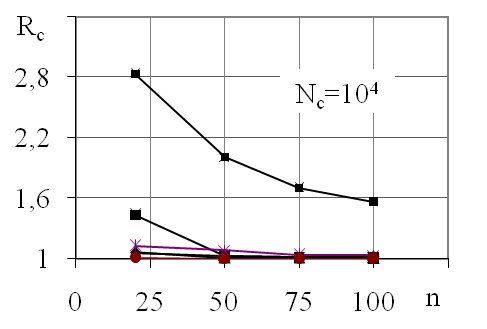
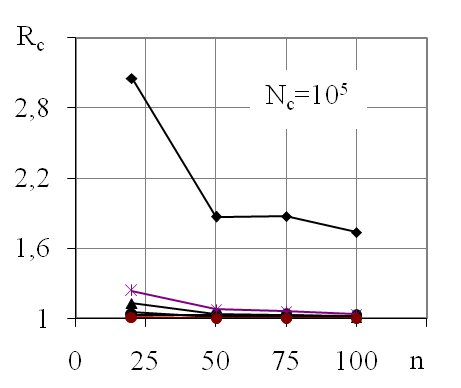
Рассмотрены разные параметры совокупностей с размахами R=1,1; 15; 18,8; 36; 50; 100; объем совокупностей составлял Nс = 103; 104; 105; 106; объем выборок n=20; 50; 75; 100; количество выборок-m=10; 50.
По полученным данным определен коэффициент Rc = Cc/X1, где Cc- параметр С совокупности; x1- минимальное значение выборки. Средние значения Rc приведены в таблице 1и построены графики (рис.2)
 |
 |
 |
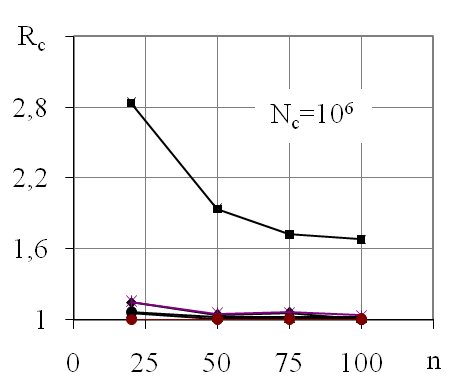 |
Рис. 2. Графики зависимости коэффициента Rc от объема выборок: 1 - совокупность с размахом 18,8; 2 - с размахом 15; 3 - с размахом 1,1; 4 –с размахом 50; 5 –с размахом 100; 6 –с размахом 35,5
Из графиков видно, что при увеличении n снижается Rc. Для размахов R=1,1;15;35,5;50;100 Rc составляет 1,05-1,4, а для размахов R=17-19 коэффициент Rc равен 1,8-3, что существенно отличается от всех остальных.
Зависимости коэффициента Rc от объема совокупности Nc приведены на рис.3.
|
a
 |
b
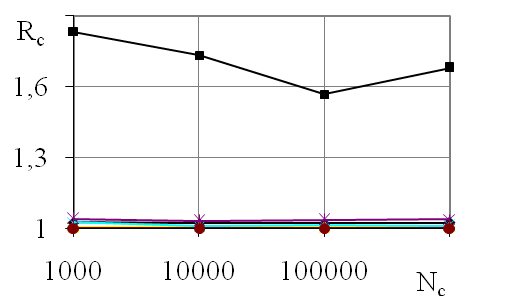 |
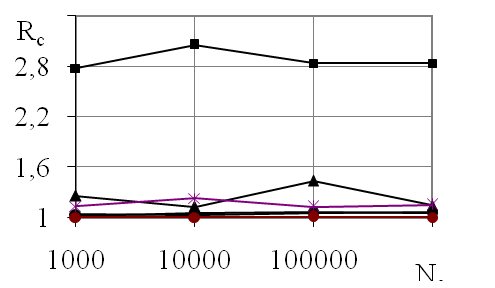
Рис. 3. График зависимости коэффициента Rc от объема совокупностей Nc: а - максимальное значение коэффициента Rc; b- минимальное значение коэффициента Rc
Анализ графиков на рис.3 показывает, что Rc для R=18,8 существенно отличается от других.
Зависимость коэффициента Rc от размаха совокупности дана на рис.4.
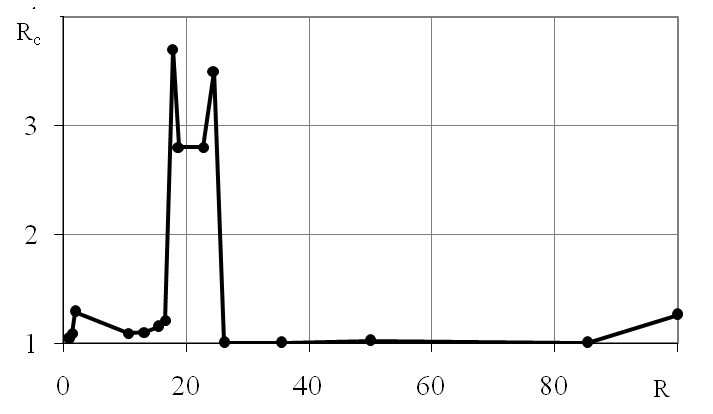
Рис.4. Зависимость коэффициента Rc от размаха R совокупностей
В интервале R=17-20 значение Rc достигает величины 2,7-4 и значительно отличается от остальных.
На рисунке 5 праведен график зависимости Rc от параметра формы Bc.
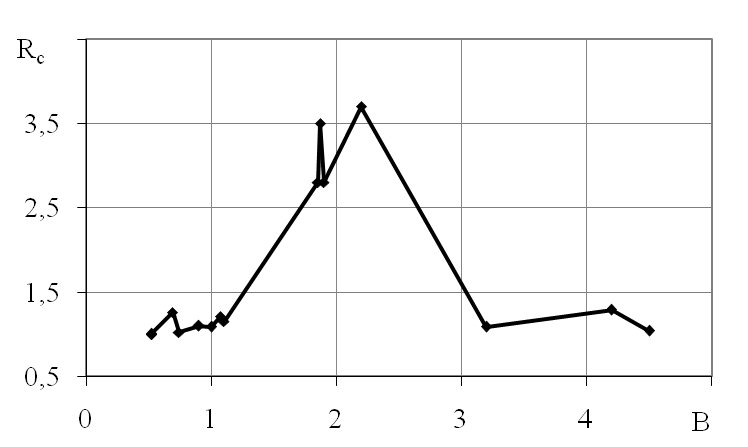
Рис. 5. График зависимости коэффициента Rc от параметра формы B совокупности
Таким образом в результате проведенных исследований выявлено, что при Bc=2,7-3,7 значения Rc возрастают с Rc=1 до Rc =3,5-3,6, что требует дополнительного анализа.
Литература
1. Касьянов В.Е. , Прянишникова Л.М., Дудникова В.В., Кузьменко А.В. Определение параметров распределения Вейбулла для совокупности по выборке прочностных характеристик сталей. Ростовский государственный строительный университет. -Ростов-на-Дону, 2006-10с.-Рус.-Деп.ВИНИТИ №389-2004 3.03.04.