Критерии равенства собственных частот колебаний чувствительных элементов микромеханических гироскопов-акселерометров

Аннотация

Лысенко И.Е., Ежова О.А.

Дата поступления статьи: 20.05.2014

Разработаны критерии согласования собственных частот колебаний чувствительных элементов двухосевых функционально интегрированных микромеханических гироскопов-акселерометров LL-типа. Рассмотрены полученные результаты моделирования.

Ключевые слова: микросистемная техника, элементная база, модель, моделирование, гироскоп, акселерометр, сенсор

05.27.01 - Твердотельная электроника, радиоэлектронные компоненты, микро- и наноэлектроника на квантовых эффектах

Разработка датчиков угловых скоростей (гироскопов) и датчиков линейных ускорений (акселерометров) является, на сегодняшний день, одним из приоритетных направлений развития микросистемной техники в мире [1 - 5].
Данные датчики нашли применение в устройствах как аэрокосмической, так и бытовой техники. Микромеханические гироскопы и акселерометры используются в резервных инерциальных навигационных системах наряду с системами ГЛОНАСС и GPS, что позволяет сохранить точность и беспрерывность навигации при потере приема сигнала со спутника [1 - 5].
Разработка многоосевых функционально интегрированных микромеханических сенсоров, позволяющих регистрировать как угловые скорости, так и линейные ускорения, является актуальной научно-технической задачей. Применение таких гироскопов-акселерометров позволяет уменьшить массогабаритные характеристики инерциальных навигационных систем и снизить их себестоимость.
На рис. 1 представлен разработанный функционально интегрированный гироскоп-акселерометр с двумя осями чувствительности [6].
Данное устройство содержит подложку 1, неподвижные электроды емкостных преобразователей (ЕПП) 2-27, неподвижные электроды электростатических приводов (ЭСП) 28-31, подвижные электроды ЭСП 32-35, балки 36-51, опоры 52-57, инерционные массы 58 и 59. Чувствительный элемент 1 образован инерционной массой 58, балками 38-41, 48-51. Чувствительный элемент 2 образован инерционной массой 29, балками 36, 37, 42, 43, 44-47.

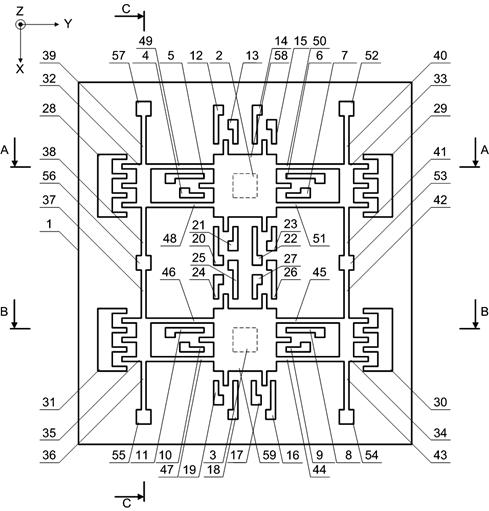
Рис. 1. Топология интегрального гироскопа-акселерометра с двумя осями чувствительности

Как показали проведенные исследования [7 - 12], параметрами, вносящими значительный вклад в величину силы Кориолиса, являются масса, амплитуда и частота колебаний чувствительных элементов устройства. Частота колебаний чувствительных элементов под действием сил электростатики будет обратно пропорциональна их массе, а под действием сил Кориолиса – обратно пропорциональна амплитуде их колебаний под действием электростатических сил. Следовательно, массу чувствительных элементов и амплитуду их колебаний под действием электростатических сил, необходимо увеличивать с целью улучшения чувствительности устройства [1, 7].
Однако увеличение массы чувствительных элементов влечет за собой увеличение занимаемой устройством площади подложки, что приводит к повышению их себестоимости. С учетом вышесказанного необходимо определить оптимальное соотношение данных параметров [1, 11].
Как отмечалось выше, сила Кориолиса зависит от частоты колебаний чувствительных элементов под действием электростатических сил. Следовательно, для повышения амплитуды колебаний чувствительных элементов под действием силы Кориолиса, необходимо чтобы частоты колебаний чувствительных элементов по всем степеням свободы были согласованы.
Как видно на рис. 1, колебания чувствительного элемента представленного устройства по осям Х и Y обусловлены одинаковой жесткость упругого подвеса и при равных значениях их длин и площадей сечения балок может быть достигнута согласованность частот колебаний по этим осям.
Из условия равенства собственных угловых частот колебаний чувствительных элементов по осям Y и Z получим критерий их согласованности:
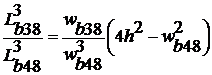, (1)                                                                  
где L_b38, L_b48, w_b38, w_b48 – длина и ширина упругих балок 38 и 48, соответственно; h – толщина.
На рис. 2 представлены зависимости отношения длин упругих балок 38 и 48 от их толщины при w_b48=5 мкм.

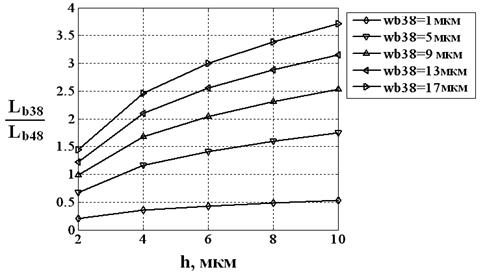
Рис. 2. Зависимость отношения длин упругих балок 38 и 48 от их толщины

На рис. 3 и 4 представлены результаты моделирования собственных угловых частот колебаний чувствительного элемента гироскопа-акселерометра. Жесткость упругого подвеса чувствительного элемента рассчитывался с учетом критерия (1).
Как видно на рис. 3 и 4 с использованием критерия (1) можно добиться согласованности частоты колебаний чувствительного элемента под действием сил электростатики с частотой колебаний по одной из осей чувствительности.
Из условия равенства собственных угловых частот колебаний чувствительных элементов по осям Х и Z получим второй критерий согласованности:
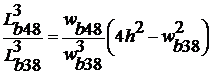.  (2)                                                                  

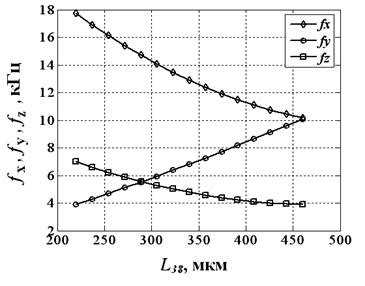
Рис. 3. Зависимость собственных частот колебаний чувствительного элемента от длины при w_b48=5 мкм, h=6 мкм и L_b48=200 мкм

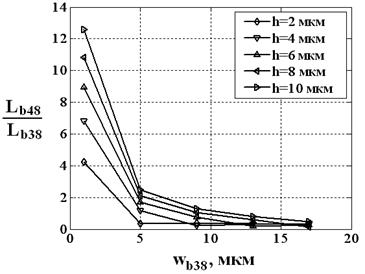
Рис. 4. Зависимость отношения длин упругих балок 48 и 38 от ширины

На рис. 5 представлены результаты численного моделирования собственных угловых частот колебаний чувствительного элемента по осям Х и Z. При этом жесткость упругого подвеса чувствительного элемента рассчитывался уже с учетом второго критерия (2).

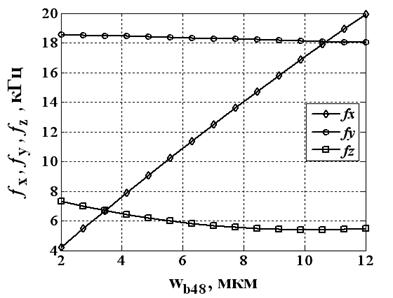
Рис. 5. Зависимость собственных частот колебаний чувствительного элемента по осям Х и Z от ширины при w_b38=5 мкм, h=6 мкм и L_b38=200 мкм

Как видно на рис. 5 с использованием критерия (2) можно добиться согласованности собственных частот колебаний чувствительного элемента по обеим осям чувствительности, что обеспечит одинаковую чувствительность устройства к угловым скоростям и линейным ускорениям. При этом согласованность собственной частоты колебаний под действием электростатических сил с собственными частотами колебаний по обеим осям чувствительности может быть достигнута использованием электростатической упругости [1, 11].
Полученные критерии равенства собственных частот колебаний чувствительных элементов под действием сил электростатики и Кориолиса по обеим осям чувствительности и полученные результаты численного моделирования могут использоваться при проектировании функционально интегрированных гироскопов-акселерометров.
Работа выполнена при финансовой поддержке Министерства образования и науки России (проекты №213.01–11/2014–12 в рамках базовой части государственного задания и №14.575.21.0045).

Литература:

1. Распопов, В.Я. Микромеханические приборы [Текст]: учебное пособие / В.Я. Распопов. – Тула: Тульский государственный университет, 2007. – 400 с.
2. Тимошенков С.П., Кульчицкий А.П. Применение МЭМС-сенсоров в системах навигации и ориентации подвижных объектов [Текст] // Нано- и микросистемная техника. – 2012. – №6. – С. 51–56.
3. Аравин В.В., Вернер В.Д., Сауров А.Н., Мальцев П.П. МЭМС высокого уровня – возможный путь развития МЭМС в России [Текст] // Нано- и микросистемная техника.– 2011. – №6. – С. 28-31.
4. Прокофьев И.В., Тихонов Р.Д. Нано - и микросистемы для мониторинга параметров движения транспортных средств [Текст] // Нано- и микросистемная техника.– 2011. – №12. – С. 48-50.
5. Анчурин С.А., Максимов В.Н., Морозов Е.С., Головань А.С., Шилов В.Ф. Блок инерциальных датчиков [Текст] // Нано - и микросистемная техника.– 2011. – №1. – С. 50-53.
6. Интегральный микромеханический гироскоп [Текст]: пат. 2266521 Рос. Федерация: МКИ7 G 01 C 19/56, G 01 P 9/04 / Б.Г. Коноплев, И.Е. Лысенко; заявитель и патентообладатель Южный федеральный университет.– № 2004117283/28; заяв. 07.06.2004; опубл. 20.12.2005, Бюл. № 35.
7. Lysenko I.E. Modeling of the micromachined angular rate and linear acceleration sensors LL-type with redirect of drive and sense axis [Text] // World Applied Sciences Journal, 2013.– №27 (6).– p.759-762.
8. Коноплев Б.Г., Лысенко И.Е., Шерова Е.В. Интегральный сенсор угловых скоростей и линейных ускорений [Электронный ресурс] // «Инженерный вестник Дона», 2010, №3. – Режим доступа: http://ivdon.ru/ru/magazine/archive/n3y2010/240  (доступ свободный) – Загл. с экрана.– Яз. рус.
9. Лысенко И.Е., Лысенко А.В. Интегральные сенсоры угловых скоростей и линейных ускорений LR-типа на основе углеродных нанотрубок [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://ivdon.ru/ru/magazine/archive/n4p2y2012/1358 (доступ свободный) – Загл. с экрана.– Яз. рус.
10. Лысенко И.Е. Моделирование двухосевого микромеханического сенсора угловых скоростей и линейных ускорений LR-типа [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://ivdon.ru/ru/magazine/archive/n1y2013/1549 (доступ свободный) – Загл. с экрана.– Яз. рус.
11. Лысенко, И.Е. Интегральные микромеханические сенсоры угловых скоростей и линейных ускорений [Текст]: Монография / И.Е. Лысенко. – Таганрог: Изд-во ЮФУ, 2013.– 180 с.
12. Elwenspoek M., Wiegerink R. Silicon micro accelerometers [Text] // Mechanical microsensors. – 2005. – p. 230-236.