Определение вариантов емкости и занятости парковок
Аннотация
В статье описываются методы прогнозирования, учитывается множество факторов, используется математическая статистика и теория вероятности. Рассматриваются различные типы вероятностных распределений, моделируются потоки автомобилей входящих и выходящих, что приближает ситуацию к реальной физической картине происходящего. Особенность работы в том – что учитывается независимость основных параметров для паркингов – моменты времени входящих автомобилей и выходящих, продолжительность нахождения на стоянке и количество занятых мест.
Рассмотрены различные варианты моделирования парковки для любых сценариев и сделаны соответствующие выводы.
Используя предложенные модели можно проводить расчеты как в локальном режиме для автомобильных парковок, так и в интеграции с влиянием парковок на общие условия движения.
Ключевые слова: парковка, занятость, очередь, терминал, модель, распределение, поток, интенсивность, вероятность, стоянка, емкость.
Для прогнозирования потребности во всех видах парковочной инфраструктуры, оценки уровня загрузки, большое значение имеет наличие информации о режимах функционирования парковок. Как правило, в зарубежных городах, где существуют системы управления парковками, эти задачи решаются на основе реальной статистической информации, и при возможности в реальном режиме времени. В то же время эта статистическая информация используется при прогнозировании уровня загрузки парковок в оперативном режиме. Анализ различных подходов к решению этих задач показывает, чем меньше информации о реальных процессах, тем более важным является использование методов прогнозирования.
При решении этой задачи необходимо учитывать множество различных факторов - время прибытия автомобилей на парковку, время нахождения на парковке, интенсивность поступающего и выходящего потока, емкость парковки, длина очереди. Кроме того, необходимо также в качестве возмущающих факторов учитывать ряд дополнительных параметров – стоимость парковки, информационное обеспечение о степени занятости парковки, наличие маршрутов общественного транспорта. Практически все эти параметры изменяются случайным образом. Поэтому для построения прогнозных моделей необходимо использовать математическую статистику и теорию вероятности.
Для создания таких моделей необходимо иметь представление о параметрах распределения прибывающих транспортных потоков, времени обслуживания, занятости парковочных мест, размерах очереди, времени ожидания. Если рассматривать логическую последовательность эксплуатации терминала или парковки, то первичным процессом является прибытие автомобилей на парковку. Практически все методики и модели используют при этом допущения, что прибытие автомобилей на парковку подчиняется Пуассоновскому распределению, а продолжительность нахождения на парковке описывается отрицательным экспоненциальным распределением. Затем обычно используется обобщенная модель многоканальной системы прибытия и нахождения автомобилей на парковке. При одном въезде на парковку все автомобили находятся в одной очереди и направляются к освободившемуся месту парковки. Основные уравнения, позволяющие вычислять длину очереди и время ожидания в различных условиях, имеют следующий вид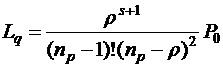 (1)
(1)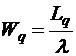 (2)
(2)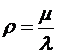 (3)
(3)
где λ – параметр интенсивности входящего потока;
µ - среднее время парковки;
np – число парковочных мест;
р0 – вероятность отсутствия автомобилей на парковке;
Lq – ожидаемое число автомобилей в очереди на парковку;
Wq – среднее время ожидания в очереди.
Подобные модели часто используются при прогнозировании парковочных процессов, однако фактически ситуация намного сложнее и поэтому необходимо рассмотреть использование кроме пуассоновского других типов вероятностных распределений. Это также важно потому, что прибытие автомобилей на парковку и продолжительность нахождения на ней могут быть статистически независимыми процессами. Поэтому, только задавая тип распределения, соответствующий конкретным условиям функционирования автомобильных стоянок и терминалов, можно прогнозировать режимы их функционирования и получать адекватные результаты.
Обращаясь к общему случаю можно определить f(x) как функцию плотности вероятности времени парковки и должно выполняться следующее уравнение для функции плотности вероятности среднего времени парковки![]()
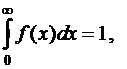 (4)
(4)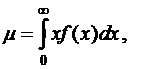 (5)
(5)
где х – продолжительность парковки каждого автомобилям в выборке;
μ – средняя продолжительность парковки всех автомобилей в выборке.
Для управления парковочными процессами необходимо моделировать как поток автомобилей, входящих на парковку, так и объем автомобилей, покидающих парковку за определенный промежуток времени. Это можно описать следующими уравнениями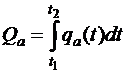 , (6)
, (6)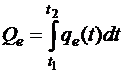 , (7)
, (7)
где Qa – общее количество автомобилей, прибывших на парковку за период моделирования;
Qa – общее количество автомобилей, покинувших парковку за период моделирования;
qa, qe – соответственно интенсивность прибывающего и уходящего с парковки потока автомобилей;
t1, t2 - начальный и конечный моменты моделирования.
Следовательно, можно определить уровень заполнения парковки, сопоставляя модели прибытия и ухода автомобилей с парковки![]() , (8)
, (8)
Или используя уравнения 6, 7 можно сформулировать более детально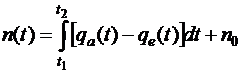 , (9)
, (9)
где n – число автомобилей на парковке в момент времени t;
n0 – число автомобилей на парковке в начальный момент времени.
Анализ применяемых методов моделирования параметров парковочных процессов показывает, что в большинстве работ не учитывается независимость основных параметров для паркингов – моментов времени входящих на автомобильную стоянку и покидающих ее транспортных средств, продолжительности нахождения на стоянке и количество занятых мест. Поэтому можно применить следующий подход при описании эксплуатации парковки. В момент времени t в интервале dt на парковку прибывает количество автомобилей, которое равно qa(t)dt. Однако, на этот же момент времени t в течение того же интервала dt парковку покидает qe(t)dt автомобилей. С использованием этих допущений можно получить следующие основные уравнения, характеризующие спрос на парковку:
- количество автомобилей на парковке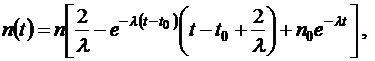 (10)
(10)
- интенсивность потока транспортных средств, покидающих парковку![]() (11)
(11)
- общее время стоянки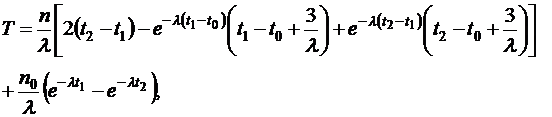 (12)
(12)
Используя приведенные модели можно осуществлять имитационное моделирование парковочных процессов для любых сценариев. Рассмотрим вариант моделирования парковки в зоне пересадочного пункта. Эти условия характеризуются достаточно большим временем парковки и пиковыми нагрузками, особенно в утренние часы. Статистика показывает, что для этих условий среднее время парковки составляет около 6-7 часов и поток входящих автомобилей в часы пик может многократно превышать средние значения. В этих условиях расчет с ориентацией на средние значения может привести к ошибкам при определении требуемой емкости парковки.
Однако использование при имитационном моделировании приведенных моделей сохраняет все особенности реальных процессов. На рис. 1, 2 приведены результаты моделирования при средней продолжительности парковки 7 часов и резком колебании входящего потока автомобилей. На рис.3, 4 приведены эти параметры для парковки в зоне торгового центра.
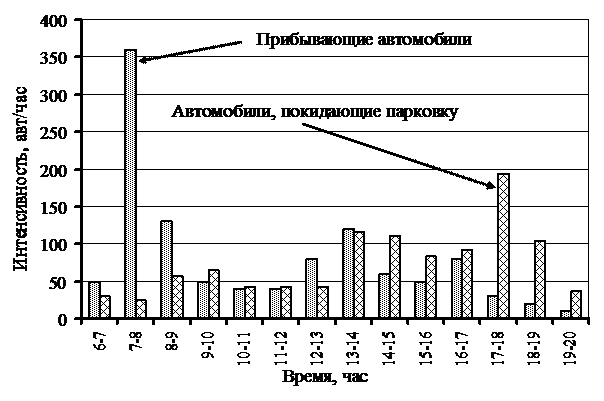
Рис. 1. Результаты моделирования прибытия и убытия автомобилей для парковки в зоне пересадочного узла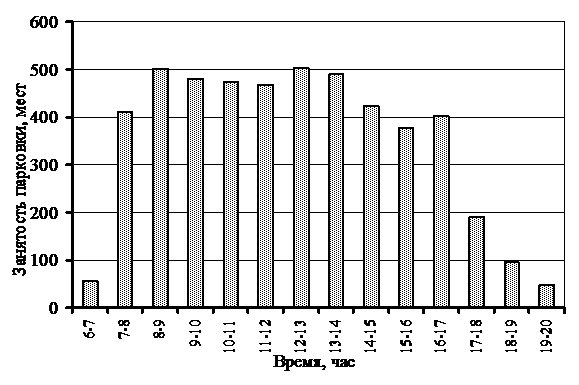
Рис. 2. Занятость парковки в зоне пересадочного узла
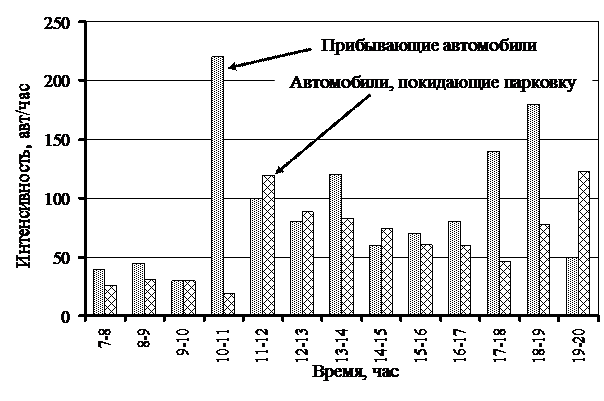
Рис. 3. Результаты моделирования прибытия и убытия автомобилей для парковки в зоне торгового центра
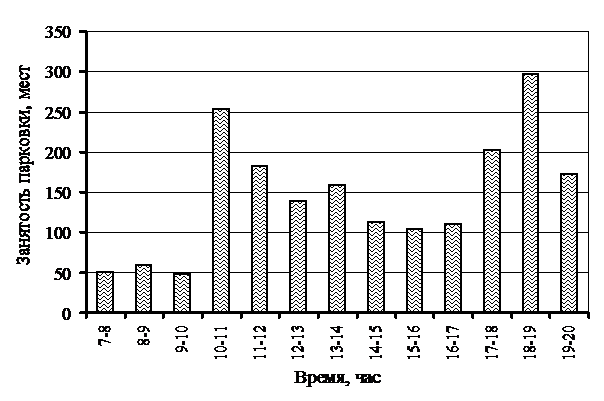
Рис. 4. Занятость парковки в зоне торгового центра
Анализируя полученные результаты можно установить, что для варианта парковки в зоне пересадочного пункта емкость парковки не должна быть менее 500 машиномест, но при расчете по средним значениям емкость парковки составит только 430 машиномест. Аналогичная ситуация и для варианта парковки в зоне торгового центра.
Рассмотренный подход к описанию парковочных процессов на основе имитационного моделирования базируется на учете вероятностных свойств системы "водитель-автомобиль-дорога-среда". Используя предложенные модели можно проводить расчеты как в локальном режиме для автомобильных парковок, так и в интеграции с влиянием парковок на общие условия движения.
Литература
1.Вол М., Мартин Б. Анализ транспортных систем. - М.: Транспорт, 1989. - 514 с.
2.Зырянов В.В., Кочерга В.Г., Поздняков М.Н. Опыт разработки комплексной схемы организации движения Ростова-на-Дону// Организация и безопасность дорожного движения в крупных городах: Сб. докладов 9-й международной научно-практ. конф., СПб, 2010, с. 72-75
3.Клинковштейн Г. И. Организация дорожного движения: учебник для вузов / Г. И. Клинковштейн, М. Б. Афанасьев. – 5-е изд., перераб. и доп. – М.: Транспорт, 2001. – 231 с.
4.Лобанов Е. М. Транспортная планировка городов / Е. М. Лобанов. – М.: Транспорт, 1989. – 240 с.
5.Lautso K. Mathematical relationships among parking characteristics and revising and reduction methods of parking field survey information. Transpn. Res. 1981, vol. 15 B, № 2, p. p. 73 – 83.