Отображение ортогональным проецированием четырехмерной гиперповерхности
Аннотация
Дата поступления статьи: 12.02.2014Решается задача исследования особенностей отображения ортогональным проецированием четырехмерной гиперповерхности, заданной уравнением в неявном виде, на одну и две гиперплоскости. Для установления связи дискриминанты гиперповерхности и огибающей предполагается, что гиперповерхность получена отображением двухпараметрического семейства двумерных поверхностей в пятимерное пространство. Проведен анализ криминант четырехмерной гиперповерхности при ее ортогональном проецировании на координатные гиперплоскости по направлениям двух координатных осей. Пересечение трехмерных гиперповерхностей (криминант) определяет двумерную поверхность, являющуюся огибающей двухпараметрического семейства двумерных поверхностей. Установлены необходимые и достаточные условия существования этой огибающей.
Полученные в общем виде результаты использованы для исследования дискриминанты четырехмерной гиперповерхности, созданной отображением двухпараметрического семейства сфер в пятимерное пространство.Ключевые слова: Семейство поверхностей, гиперповерхность, огибающая, особенность отображения, дискриминанта.
ФГБОУ ВПО «Омский государственный технический университет»
Во многих прикладных задачах, связанных с профилированием режущего инструмента, определяют огибающую семейства поверхностей. Наряду с классическим подходом [1 - 2] к определению огибающей, в последнее время используется и новый [3], использующий отображение ортогональным проецированием поверхности на плоскость: [4 - 6] и другие. Так, если спроецировать график однопараметрического семейства двумерных поверхностей в пространство R4, то получим некоторую трехмерную гиперповерхность Σ. Дискриминанта этой гиперповерхности является огибающей рассматриваемого семейства. Исследование поверхности Σ при задании ее параметрическими уравнениями и уравнением в неявной форме проведено в работах [7 - 8], а его применение – в работах [9 - 10].
Отображение ортогональным проецированием четырехмерной поверхности и использование полученных результатов к определению огибающей двухпараметрического семейства поверхностей рассматривается ниже.
Пусть исходная четырехмерная гиперповерхность![]() задана уравнением в неявном виде
задана уравнением в неявном виде
![]() (1)
(1)
Рассмотрим отображения ортогональным проецированием этой поверхности по направлениям осей u и v на соответствующие координатные гиперплоскости.
Уравнения гиперплоскостей, касательных к гиперповерхности (1) в некоторой ее точке M(x0,y0, z0, u0,v0), записываются в виде
![]() (2)
(2)
В точках гиперповерхности, в которых касательные гиперплоскости параллельны оси 0U, выполняется условие
![]() (3)
(3)
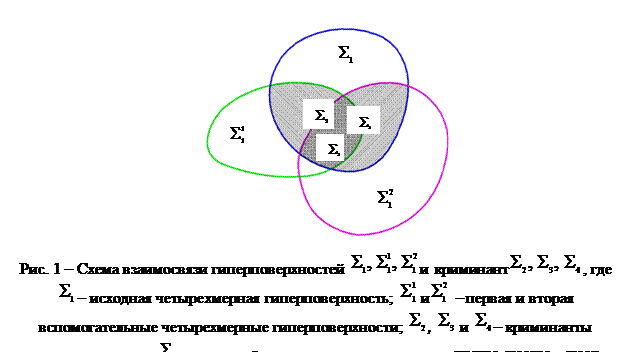
Будем рассматривать (3) как уравнение первой вспомогательной четырехмерной гиперповерхности ![]() Пересечение гиперповерхностей (1) и (3) определяют трехмерную гиперповерхность
Пересечение гиперповерхностей (1) и (3) определяют трехмерную гиперповерхность ![]() (рис.1), являющуюся криминантой гиперповерхности
(рис.1), являющуюся криминантой гиперповерхности ![]() при ее ортогональном отображении вдоль оси u.
при ее ортогональном отображении вдоль оси u.
Четырех параметрическое множество плоскостей, касательных к гиперповерхности ![]() (3) в ее некоторой точке N(x0,y0, z0, u0,v0), записывается в виде
(3) в ее некоторой точке N(x0,y0, z0, u0,v0), записывается в виде
![]() (4)
(4)
Гиперплоскости (2) и (4) пересекаются по трехмерным гиперплоскостям, касающимся гиперповерхности ![]() . В точках гиперповерхности (1), в которых касательные гиперплоскости параллельны оси 0V, выполняется условие
. В точках гиперповерхности (1), в которых касательные гиперплоскости параллельны оси 0V, выполняется условие
![]() (5)
(5)
Полученное уравнение рассматриваем как уравнение второй вспомогательной четырехмерной гиперповерхности ![]() Пересечение четырехмерных гиперповерхностей (1) и (5) определяет трехмерную гиперповерхность
Пересечение четырехмерных гиперповерхностей (1) и (5) определяет трехмерную гиперповерхность![]() , являющуюся криминантой гиперповерхности
, являющуюся криминантой гиперповерхности ![]() при ее ортогональном отображении вдоль оси 0V . Тогда четырех параметрическое множество плоскостей, касающихся гиперповерхности (5) в ее некоторой точке K(x0,y0,z0, u0,v0), записывается уравнением в виде
при ее ортогональном отображении вдоль оси 0V . Тогда четырех параметрическое множество плоскостей, касающихся гиперповерхности (5) в ее некоторой точке K(x0,y0,z0, u0,v0), записывается уравнением в виде
![]() (6)
(6)
Пересечение трехмерных гиперповерхностей ![]() и
и![]() задает двумерную поверхность
задает двумерную поверхность ![]() , являющуюся криминантой гиперповерхности (1) при ее ортогональном отображении на гиперплоскость XYZ(по двум направлениям вдоль осей u и v).
, являющуюся криминантой гиперповерхности (1) при ее ортогональном отображении на гиперплоскость XYZ(по двум направлениям вдоль осей u и v).
Пусть точки M, N и K принадлежат не только соответствующим гиперповерхностям, но и двумерной поверхности ![]() . Тогда касательная плоскость к этой двумерной поверхности определяется в пересечении гиперплоскостей (2), (4), (6). Рассматривая уравнения (2) и (4) как систему линейных уравнений относительно (u-u0) и (v-v0), получим
. Тогда касательная плоскость к этой двумерной поверхности определяется в пересечении гиперплоскостей (2), (4), (6). Рассматривая уравнения (2) и (4) как систему линейных уравнений относительно (u-u0) и (v-v0), получим
![]()
где ![]()
![]()
![]()
После подстановки полученных выражений в равенство (6), получим уравнение касательной плоскости к поверхности ![]()
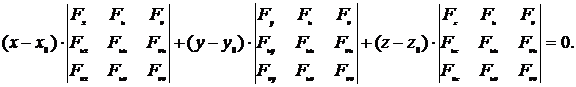 (7)
(7)
Тогда из приведенных уравнений следует, что криминанта гиперповерхности (1) при ее отображении ортогональным проецированием на гиперплоскости по направлениям осей 0U и 0V, определяется системой уравнений (1), (3) и (5), при условиях
![]() и
и 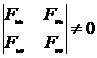 .
.
В качестве примера, иллюстрирующего достоверность полученных результатов, рассмотрим четырехмерную гиперповерхность, определяемуюуравнением
![]() (8)
(8)
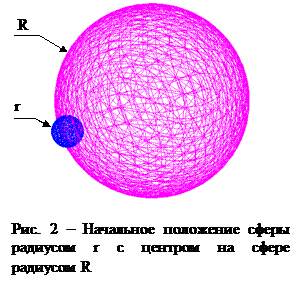
Эта гиперповерхность получена отображением двухпараметрического семейства сфер радиуса r c центрами на сфере радиуса R (рис.2) в гиперпространство XYZVU .
Тогда в соответствии с (3) уравнение первой вспомогательной гиперповерхности будет
![]() (9)
(9)
Откуда имеем
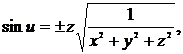
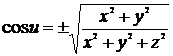 . (10)
. (10)
После подстановки зависимостей из (10) в равенство (9), получим уравнение трехмерной гиперповерхности, являющейся криминантой гиперповерхности (1) при ее отображении на гиперплоскость вдоль оси 0V:
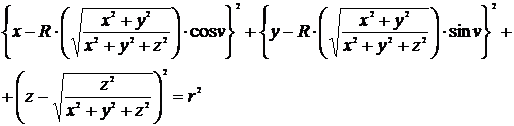 (11)
(11)
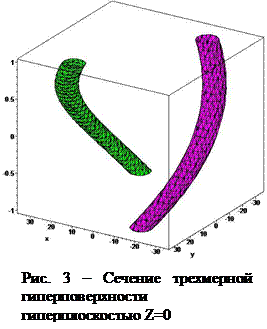
Для исследования этой гиперповерхности рассечем ее гиперплоскостями. Так для Z=0, имеем
![]()
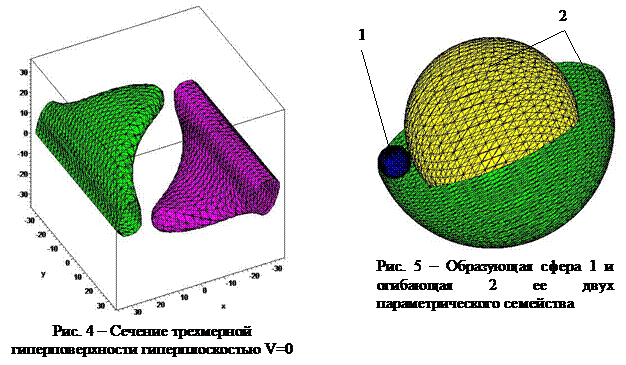
Графиком этого уравнения является двумерная циклическая поверхность с плоскостью параллелизма 0XY(рис. 3). Сечением гиперповерхности (11) гиперплоскостью V=0 является двумерная поверхность, определяемая уравнением
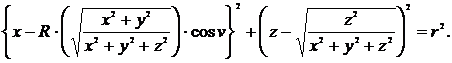
Ее график представлен на рис. 4.
Рассмотрим теперь отображение гиперповерхности (1) вдоль оси 0U. Вэтом случае уравнение второй вспомогательной гиперповерхности в соответствии с (5) получим в виде
![]() (12)
(12)
Откуда
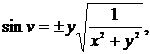 а
а 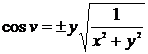 . (13)
. (13)
Трехмерная гиперповерхность (12) является криминантой гиперповерхности (1) при ее отображении вдоль оси 0U. Криминанта гиперповерхности (1) при ее отображении вдоль осей 0U и 0V находится в пересечении первой и второй трехмерных гиперплоскостей. После подстановки выражений из (10) и (13) в (9) уравнение этой криминанты будет
![]() (14)
(14)
Графиком этого уравнения являются две сферы с центром в начале системы координат и радиусами (R+r) и (R-r) (рис. 5). После преобразований уравнение (14) можно представить в виде![]()
Это уравнение определяет алгебраическую поверхность четвертого порядка. Она распадается на две поверхности второго порядка – две сферы.
Таким образом, проведенные исследования гиперповерхности и ее отображения ортогональным проецированием на координатные гиперплоскости позволили получить в общем виде огибающую двухпараметрического семейства поверхностей, а также необходимые условия ее существования.
Полученные результаты апробированы на модели четырехмерной гиперповерхности, полученной отображением двухпараметрического семейства сфер в пятимерное пространство. Приведены как аналитические зависимости, так и соответствующие компьютерные полигональные модели сечений трехмерной гиперповерхности и двухмерной дискриминанты четырехмерной гиперповерхности.
Литература:
- Лашнев, С. И. Расчет и конструирование металлорежущих инструментов с применением ЭВМ [Текст]. / С. И. Лашнев, М. И Юликов. – М.: Машиностроение, 1975. – 392 с.
- Litvin, F. L. Alfonso Fuentes Geometry and Applied Theory / Litvin, F. L. – Cembridge University Press, 2004. – 816 p.
- Thom, R. Sur la theorie des envelopes / R. Thom // J. de math. pur et apple. – 1962. – Vol. 41. – № 2. – Р. 177-192.
- Арнольд, В. И. Особенности гладких отображений [Текст]. – Успехи мат. наук. – 1968. – т.XXIII, вып. 1(139) – С. 4–44.
- Брус, Дж. Кривые и особенности. / Дж., Брус, П. Джиблин [Текст]. – М.: Мир, 1988. – 262 c.
- Платонова, О. А. Проекции гладких поверхностей [Текст]. / О. А. Платонова // Тр. Семинара им. И.Г. Петровского. – 1984. – т. 10. – С. 135-149.
- Ляшков, А. А.Отображение ортогональным проецированием гиперповерхности на гиперплоскость [Текст]/ А. А. Ляшков, В. Я. Волков // Вестник Иркутского Государственного Технического Университета. – 2012. – № 2. – 18-22 с.
- Ляшков, А. А. Отображение ортогональным проецированием поверхности, заданной параметрическими уравнениями [Текст] / А. А. Ляшков // Омский научный вестник. – 2012. – № 2(110). – 9-13 с.
- Ляшков, А. А. Формообразование винтовой поверхности детали угловой фрезой [Электронный ресурс] / А. А. Ляшков // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/978 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Ляшков, А. А. Семейство поверхностей, заданное формулами преобразования координат, и его огибающая [Электронный ресурс] / А. А. Ляшков, А. М. Завьялов // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1512 (доступ свободный) – Загл. с экрана. – Яз. рус.